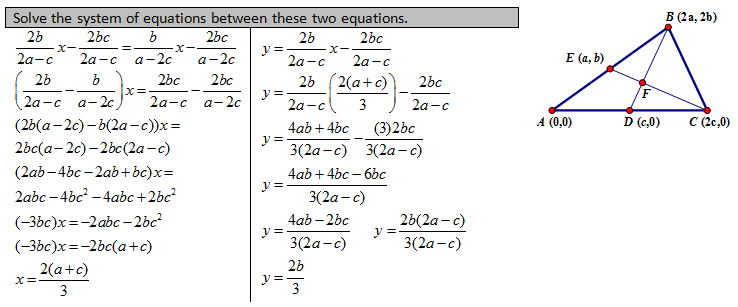CONCEPT 1 -- Prove theorems about triangles.
| TEACHER NOTE -- I have provided a number of different ways to prove each of these concepts. Classic or traditional ways that we have been doing them for 100's of years and then some new ways using transformations. I have also attempted to show some informal ways as well as formal ways... depending on the complexity that you want to handle this topic with. |
(1) Prove that the interior angles of a triangle sum to 180°.
a) Triangle Dissection (Informal – Classic Approach)
An informal proof that is often used is the process of having our students create a triangle on a piece of paper, naming the three angles A, B, and C and then cutting out the triangle. When the triangle is cut out, the student should rip off the three angles, placing them together, vertex to vertex. They will see that the three angles form a straight line. Therefore, the sum of the three interior angles of a triangle is 180°.
b) An Auxiliary Parallel Line (Formal – Classic Proof)
A formal two column proof of this theorem is done using the angle relationships found with parallel lines and a transversal. Since these angle relationships were established in objective G.CO.9, we are now able to apply them.

c) Proof by Translation (Formal – Transformational Approach)
| TEACHER NOTE -- I like this one.... simple ideas but a new approach.... |
Given: ΔABC
Prove: m∠1 + m∠2 + m∠3 = 180° |
 |
| |
|

|
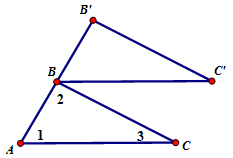 |
d) Proof by Rotation (Formal – Transformational Approach)
Given: ΔABC
Prove: m∠1 + m∠2 + m∠3 = 180° |
 |
| |
|
 |
 |
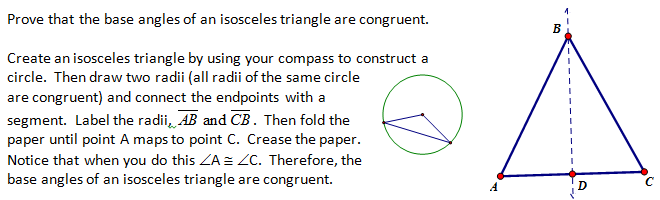
(2) Prove that Base Angles of an Isosceles are Equal (Isosceles Triangle Theorem)
a) Proof by Angle Bisector (Formal -- Classic Approach)

b) Proof by Perpendicular Bisector (Formal – Classic Approach)

c) Proof by Paper Folding (Informal Proof – Transformational Approach)
d) Proof by Symmetry (Informal – Transformational Approach)

e) Proof by Transform (Formal – Transformational Approach)

3. Prove the Midsegment Theorem (that the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length)
| TEACHER NOTE -- It seems that the three most popular ways to prove this theorem use concepts presented in objectives; G.CO.11 (parallelogram properties), G.SRT.3 (Similar Triangles), and G.GPE.4 (Coordinate Proof). Therefore, this theorem may be revisited numerous times throughout the course. |
a) Proof by Parallelogram Properties (Formal – Classic Approach)


b) Proof by Similarity (Formal – Classic Approach)

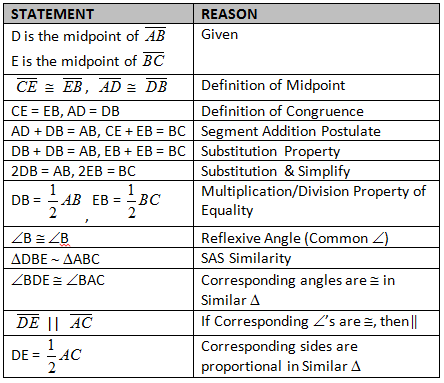
c) Proof by Coordinates (Formal – Classic Approach)
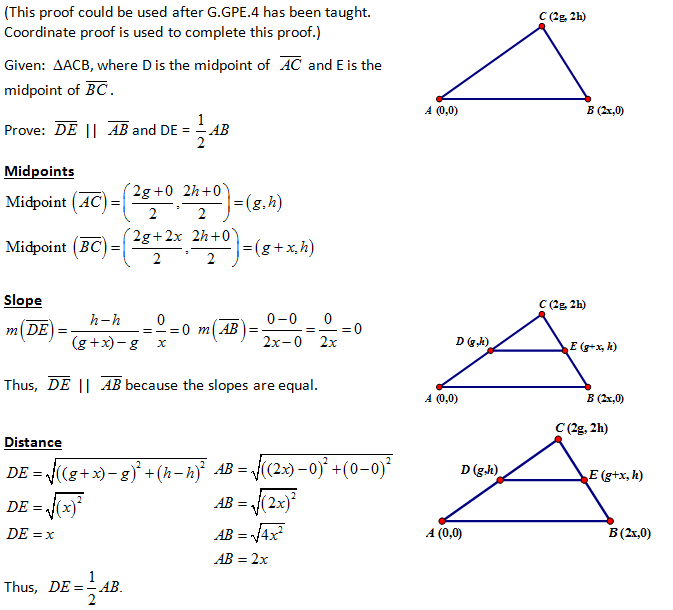
d) Proof by Translation (Formal – Transformational Approach)
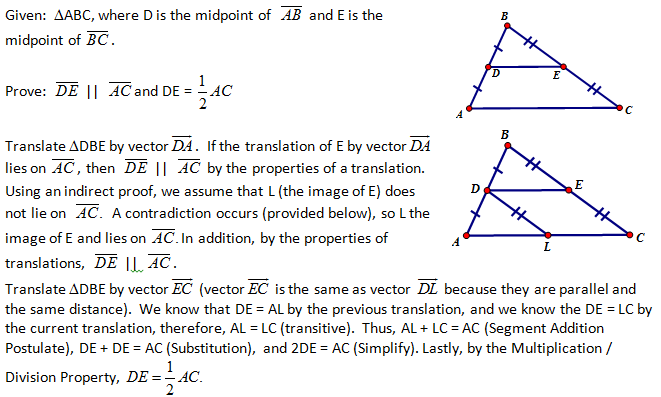
| TEACHER NOTE -- I wish I could avoid having to introduce this indirect proof here but I could not assume that E would simply land on segment AC after the translation. |

e) Proof by Double Translations (Informal – Transformational Approach)
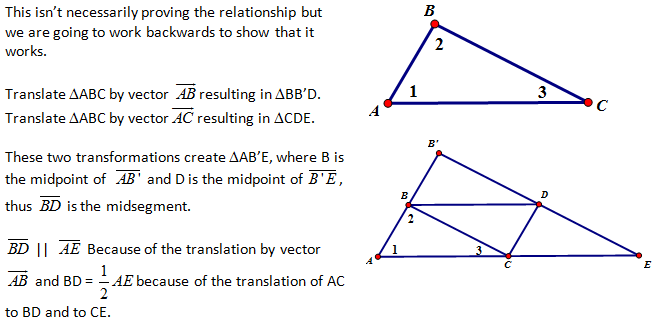
f) Proof by Construction (Informal – Investigative Approach)
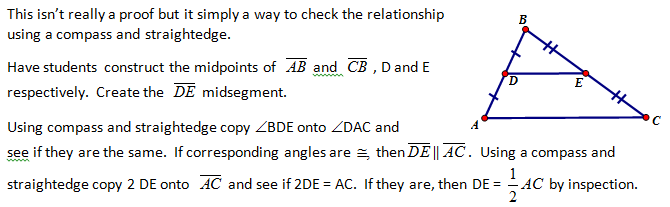
4. Prove that the medians of a triangle meet at a point.
| TEACHER NOTE -- Of these proofs I like this one the best. Quite straight forward and it doesn't assume concurrency. |
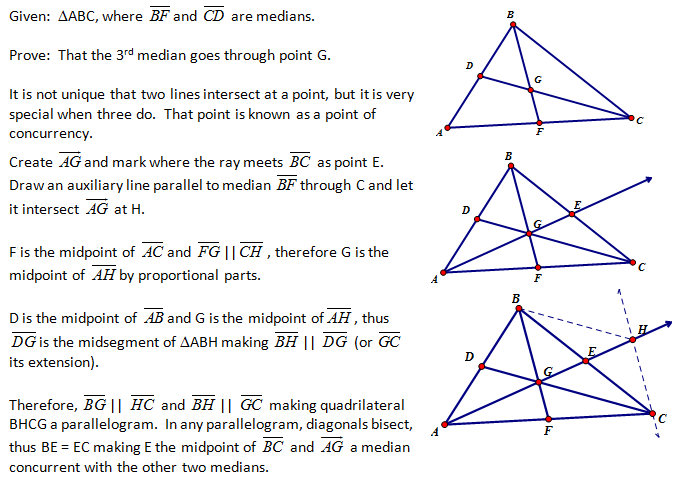
a) Proof by Midpoint (Formal – Classic Approach)
This approach uses the proportional parts relationship (G.SRT.4) and properties of a parallelogram (G.CO.11). Therefore, this approach must wait to be presented until these concepts have been covered.
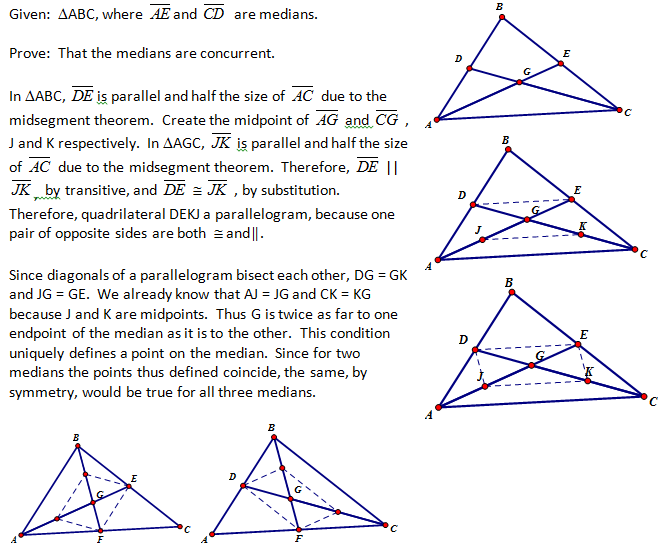
b) Proof by Midsegment (Formal – Classic Approach)
This approach uses properties of a parallelogram (G.CO.11). Therefore, this approach must wait to be presented until these concepts have been covered.
c) Proof by Coordinates (Formal – Classic Approach)


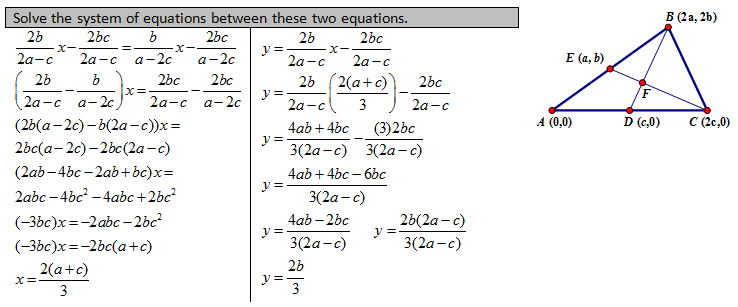


|