OBJECTIVE - G.SRT.D.10

Prove the Law of Sines and the Law of Cosines and then use them to solve problems.

INTERPRETATION OF OBJECTIVE - G.SRT.D.10

No interpretation needed - prove the Law of Sines and the Law of Cosines and then solve problems using them. Of course hidden inside this very short objective is the ambiguous case for the Law of Sines. That can be a difficult concept for students to see and understand.

SKILLS

(1) The student will be able to solve a triangle using the Laws of Sines and/or the Law of Cosines.

(2) The student will be able to explain the cases of AS₁S₂.

(3) The student will be able to determine which relationship (Law of Sines/Law of Cosines) is required for solving the triangle.

THE BIG IDEA

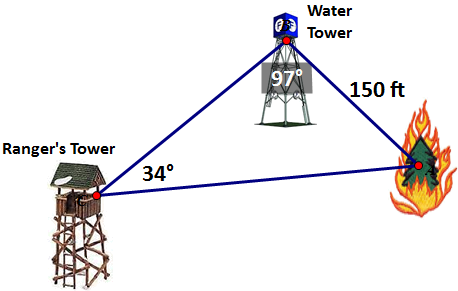
The big idea is that using the basics of trigonometry we are able to derive two very powerful relationships that allow us to solve for sides and angles of ANY TYPE of triangle. The two laws provide us with incredibly powerful formulas to solve many real world problems.

TRAPS & PITFALLS

Yikes... this is a minefield of pitfalls and traps. The Law of Sines is very simple when working with the congruency relationships of ASA and AAS but becomes much more complex when working with AS₁S₂. The relationship AS₁S₂ comes with a number of different cases, and one of those cases produces more than one possible set of answers. The road sign should say "SLOW DOWN - CAUTION DIFFICULT CONCEPTS AHEAD". The ambiguous case also requires students to understand the relationship learned in G.SRT.9 that sin b = sin (180 - b). This is also the first time a student would have seen a negative value for a ratio such as cos b = -0.3432. This causes a few moments of explaining as well. Most all of our trigonometry experience at this level has been non-coordinate based but these relationships require us to introduce those coordinate relationships to make these moments make sense.

PAST CONNECTIONS

The Laws of Sine and Cosine are extensions of the basic trigonometry relationships discussed earlier. Those right triangle trigonometry relationships form the basis for deriving the new laws and applying them in oblique triangles.

FUTURE CONNECTIONS

These laws allow us to solve for any angle or side of ANY triangle. These are very powerful relationships that get used in many places.

MY REFLECTIONS (over line l)

This is an honors topic for a reason. It takes some pretty good processing skills to put all of this together. I guess my big suggestion is to deal with this issue back when you introduce G.CO.8 concerning the congruence criteria for triangles. Things at that stage aren't very difficult so to take some time then to discuss why AS₁S₂ by itself is not a congruence theorem pays off HUGE at this point of the year. In the last two years I have included AS₁S₂ when S₂ > S₁ as a congruency criteria. This has helped me discuss the cases in much more detail and by the time we get to this stage of the year things are much more expected and normal.