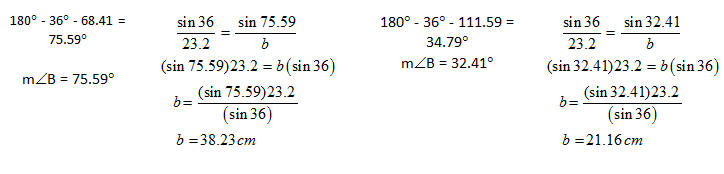CONCEPT 1 – Prove the Laws of Sines.
As mentioned in the previous objective up until this time we have been working with right triangles but now we are starting to expand the use of trigonometry to all triangles, even oblique triangles. In this objective we will show that if any three of the six measures of triangle are given (provided at least one measure is a side), then the other three measures can be found.
One of the considerations when doing this, is if the three pieces of information force congruence or not. So for example if we are given SAS, ASA, AAS/SSA, SSS and some cases of AS1S2 we know that the information is enough to guarantee congruence in the triangle.
The first new relationship in this objective that we are going to derive is called the Law of Sines. We will follow similar logic to how we handled our new area formula.
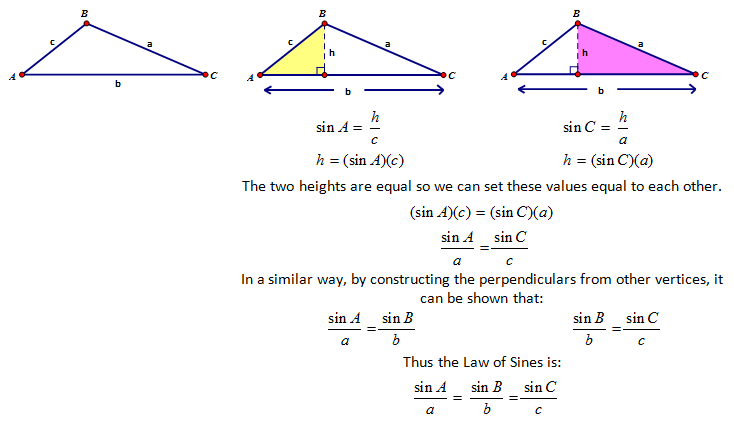
| The Law of Sines is written in more than one form... sometimes the side lengths are in the numerator position and the sine vallues is in the denominator. It seems to be simply a preference because obviously it makes no difference. |
The Law of Sines is a proportion that compares the sine of the angle to the length of its opposite side. Solving this type of problem can be quite easy but it does only work in certain situations because an angle and its corresponding opposite side need to be known to form the ratio thus we need ∠A & a or ∠B & b or ∠C or c.
The Law of Sines will work for the following situations: ASA, AAS and AS1S2. The first two cases are congruence cases so when we solve for the missing information we are guaranteed to all get the same answers.
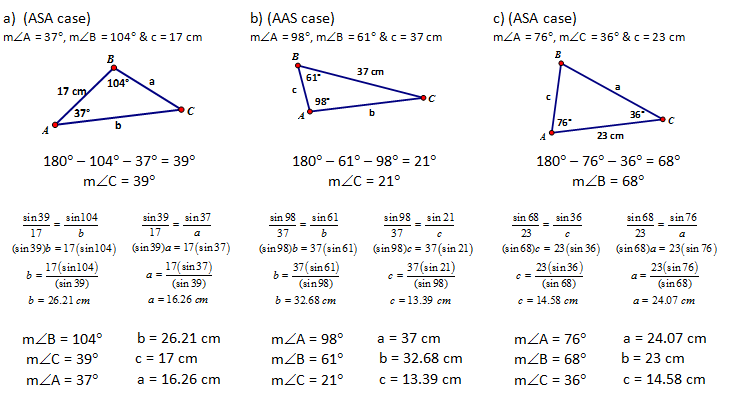
Let’s try a couple examples of the congruence cases of ASA and AAS. Solve for all angles & sides in the Δ.
Notice that because the Law of Sines is a proportional relationship that:
Largest Angle is always opposite the Longest Side (& vice versa)
Smallest Angle is always opposite the Shortest Side (& vice versa) |
| Good Luck... Here comes some tricky stuff... Back in GCO.8 I spent time discussing the AS1S2 so that when I get here it isn't totally a new concept. |
The other case that works for the Law of Sines is AS1S2 but if you remember in G.CO.8 we discussed some of the issues that are present in that case – not all cases of AS1S2 are congruence relationships. Because of this we have to again discuss the case by case situations of AS1S2 and relate them to the Law of Sines.
CASE #1 – AS1S2, when S2 is greater than S1.

This forms a triangle congruence relationship. There is only one way for S2 to be placed to complete the triangle. Because this is a congruence relationship a single answer will be present when solving – let us do an example.
Solve for all angles & sides in the Δ, given that m∠A = 47°, a = 20 cm and c = 12 cm.

CASE #2 – AS1S2, when S2 is less than S1. (Too Short)
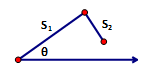
This is a weird case but when establishing all things that could happen we need to include this. It is possible that S2 is not long enough to close the triangle. This of course is not a congruence relationship, it doesn’t even form a triangle. So how will you know if it is this situation… the numbers will tell you .
Solve for all angles & sides in the Δ, given that m∠A = 73°, a = 8 cm and c = 14 cm.

CASE #3 – AS1S2, when S2 is less than S1. (1 Intersection)

This case is typically known as HL, which stands for Hypotenuse – Leg. It gets this special name because it is the right triangle that locks this shape. A way to understand why this forms a congruence relationship is because in a right triangle if you know two sides, you can use the Pythagorean Theorem to calculate the third side. HL forms a triangle congruence relationship. No example given here because when you solve for the angle it will reveal itself to be 90° and you will then be in a right triangle.
Now the final case – Known as the AMBIGUOUS CASE. Ambiguous basically means…to be uncertain or more than one correct value – it gets this name because there are two possible triangles and thus there are two sets of answers possible. If you encounter this special case, you are to completely solve for BOTH triangles.
CASE #4 – AS1S2, when S2 is less than S1. (2 Intersections)

| Well here it is.... the Ambiguous case... the art of success here is helping students to recognize when it exists. Most students become very skilled with the Law of Sines but recognizing this case is the difficult part. If they know the other cases of AS1S2, when S2 is less than S1 definately help to narrow down the possible things that can happen. |
This is known as the AMBIGUOUS CASE because two different triangles can be formed by this information. Because S2 is shorter it can swing to form two possible locations. This does NOT form a triangle congruence relationship.

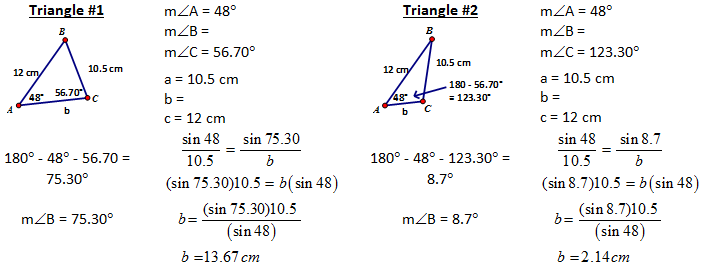

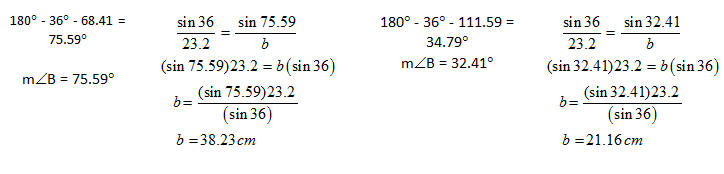
|