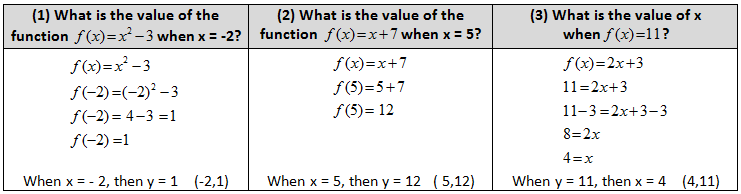CONCEPT 1 – Describe transformations as functions that take points in the plane as inputs and give other points as outpoints.
| TEACHER NOTE -- The key to this area is to connect the input/output process developed with functions in Algebra, to the coordinate rules found in geometry. |
QUICK ALGEBRA REVIEW
In algebra we studied functions extensively and during that time we learned how to solve for variables using function notation. Let me show you a few examples to remind you.
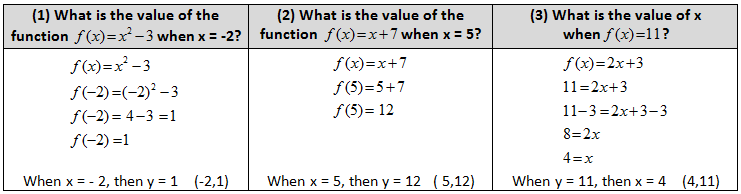
In the first two examples we were given the x value and then asked to solve for the y value (the value of the function). In the third example we were given with the y value (the value of the function) and then asked to work backwards to determine the x value that would have produced that result.
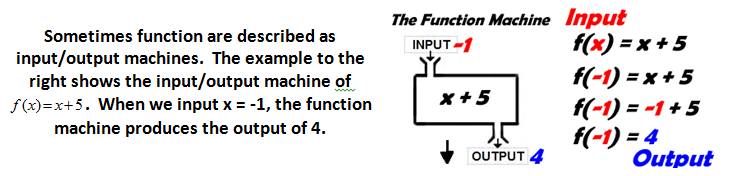
CONNECTION TO GEOMETRY
In geometry we have a similar input/output process when we determine how shapes are altered or moved. Geometric objects can be moved in the coordinate plane using a coordinate rule. These rules can alter the shape in many different ways. Some rules will translate the shape, some will rotate or reflect the shape, some will stretch or distort the shape, some will increase the size of the shape, etc… lots of different things can happen. Coordinate rules come in the following form:

So rule T will move or map all points (x,y) by adding 3 to the x value of each point, and subtracting 6 from each y value of each point.
| TEACHER NOTE -- This is where you introduce the notation of A and A' (A prime). This is also where we discuss the new terms of pre-image and image. I have always disliked the term 'pre-image', for years I used original and image but the problem with this is that when many transformations take place and then you would have many originals... this doesn't make sense. It does make sense that every image has a pre-image (the one that came before this one). |
The name of the rule is a capital letter before the (x,y). The point (x,y) represents that all points in the plane will be effected by this rule. The arrow represents the geometric term of map or mapping, which is a geometric way of saying moves. Finally the coordinate description after the mapping arrow symbol represents the change produced by the rule. Can you see the connection to functions? You will input values into the coordinate rule and it will output new values, just as function did. A change is that we refer to the input value as the pre-image, the original location of the point, and the output value as the image, the new location of the point. To help clarify the difference between a pre-image and an image, we use special notation. If the pre-image is point A, then its image will be A’ (said A prime). The prime notation tells us that it is an image.
Let me do a few examples to help you see the correlation between algebra and geometry.

Both of these examples provided the pre-image (input) values and then asked you to solve for the image (output value). We can work backwards through the process; just as in we did with the function example #3. Let us look at two where we know the image and we work backwards through the coordinate rule to solve for the pre-image.
| TEACHER NOTE -- Working backwards is ALWAYS MORE DIFFICULT!! Most students will see that 'working backwards' is performing the inverse opperation. So if you were adding, you subtract, if you were multiplying, you divide, etc..... |

CONCEPT 2 – A transformation is a one to one function.
Function & Mapping -- The word mapping is used in geometry as the word function is used in algebra. While a mapping is a correspondence between sets of points, a function is a correspondence between sets of numbers. Function and Mapping mean the same thing but just in two different contexts, in Algebra and in Geometry.
| TEACHER NOTE -- This gets a little technical but certainly links functions & one to one functions to geometry through mapping and transformations. I just wanted to clarify two terms that we will use 1000 times each during this year (mapping and transformations). |
A correspondence between two sets A and B is a FUNCTION of A to B IF AND ONLY IF each member of A corresponds to one and only one member of B.
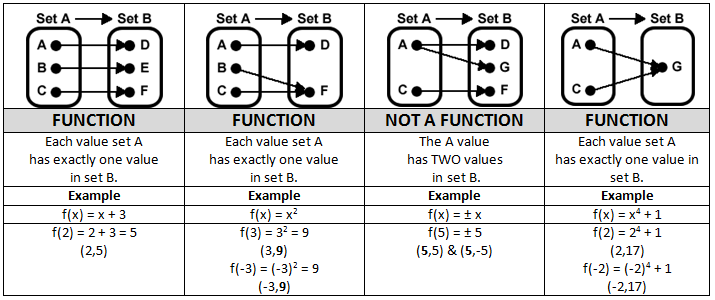
A correspondence between the pre-image and image is a MAPPING IF AND ONLY IF each member of the pre-image corresponds to one and only one member of the image.
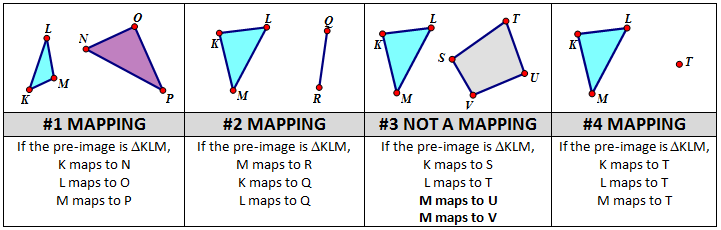
While examples #2 and #4 are mappings, they would not be very useful. We don’t want to start with a triangle and end up with a segment or a point after we map them. We want to study the mappings that preserve the number of points between the pre-image and image. In Algebra when there is exactly the same number of elements in the domain as there is in the range it is called a ONE TO ONE FUNCTION. In geometry, when you same the same number of points in the pre-image as in the image, it is called a TRANSFORMATION.

Transformations and One to One Correspondence Functions
A transformation is a one to one correspondence between the points of the pre-image and the points of the image. We will only be studying transformations. A transformation guarantees that if our pre-image has three points, then our image will also have three points.
CONCEPT 3 – Compare transformations that preserve distance and angle (i.e. rigid motions) to those that do not (e.g. translation vs. horizontal stretch).
An ISOMETRIC TRANSFORMATION (RIGID MOTION) is a transformation that preserves the distances and/or angles between the pre-image and image.
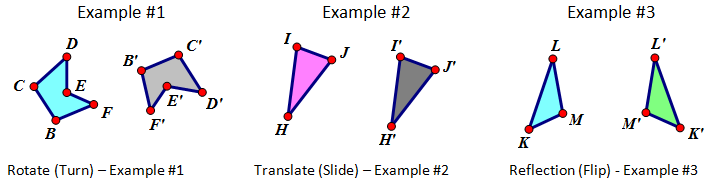
A NON-ISOMETRIC TRANSFORMATION (NON-RIGID MOTION) is a transformation that does not preserve the distances and angles between the pre-image and image.
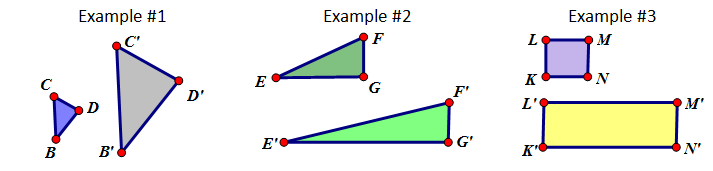
Stretch – Where one dimension’s scale factor is different than the other dimension’s scale factor. Examples #2 and #3 represent stretches. A stretch definitely distorts the shape making it a NON-ISOMETRIC transformation.
Dilation – Where both dimension’s scale factors is the same. The shape is proportional, not identical. A dilation changes the size of the shape making it a NON-ISOMETRIC transformation.
There are many ways to distort a shape but these two are the most popular.
| TEACHER NOTE -- There are many ways to distort a shape but still mantain a transformation between image and pre-image. Shearing is one that is not mentioned here but it is also a non-isometric transformation. |
|