CONCEPT 1 – Given a shape describe the rotations and reflections that carry it onto itself.
To carry a shape onto itself is another way of saying that a shape has symmetry. There are three types of symmetries that a shape can have: line symmetry, rotation symmetry and point symmetry. Let us look at each of these.
| TEACHER NOTE -- Line symmetry is obviously linking us to reflections. It is also going to help us when we want to determine properties of shapes. Line symmetry will help us establish that the base angles of an isoscles are congruent or diagonals of a rectangle are congruent. |
LINE SYMMETRY (or REFLECTIONAL SYMMETRY)

I personally like definitions #2 and #4 where line symmetry is defined in terms of a reflection. Below are some examples of figures that do have line symmetry. A shape can have more than one line symmetry.
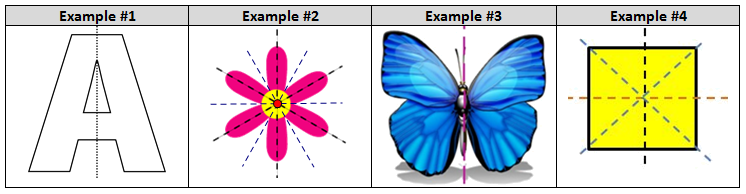
Here are a few non-examples of shapes DO NOT have line symmetry.
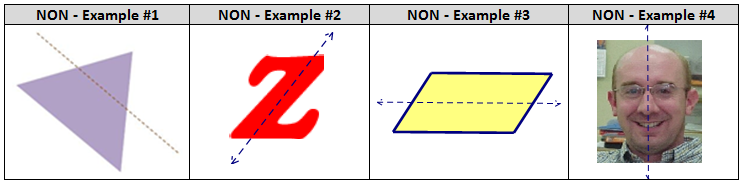
| TEACHER NOTE -- The rectangle and the parallelogram are often done incorrectly. Work through this with the students. |
The CLASSIC ERROR with line symmetry is the rectangle. Student often draw a line of symmetry along the diagonal as shown below IT DOES NOT PRODUCE a line of symmetry. Vertical and horizontal lines of symmetry seem to be easy for students to see but diagonal (or sloped) ones cause a lot more trouble visually.

The maximum lines of symmetry that a polygon can have are equal to its number of sides. The maximum is always found in the regular polygon, because all sides and all angles are congruent.
ROTATIONAL SYMMETRY
Definition
A geometric figure has rotational symmetry if the figure is the image of itself under a rotation about a point through any angle whose measure is strictly between 0° and 360°. 0° and 360° are excluded from counting as having rotational symmetry because it represents the starting position.
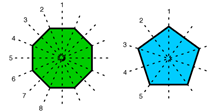
Here are some examples of shapes that have rotation symmetry.

ANGLE OF ROTATION - When a shape has rotational symmetry we sometimes want to know what the angle of rotational symmetry is. To determine this we determine the SMALLEST angle through which the figure can be rotated to coincide with itself. This number will always be a factor of 360°. So in the examples above, example #1 would have angle of rotational symmetry of 120°, example #2 would have an angle of 180°, example #3 would have an angle of 120° and finally example #4 would have an angle of 180°.
ORDER OF A ROTATION SYMMETRY -- The number of positions in which the object looks exactly the same is called the order of the symmetry. When determining order, the last rotation returns the object to its original position. Order 1 implies no true rotational symmetry since a full 360 degree rotation was needed.
So in the four examples of rotation symmetry, example #1 has order 3, example #2 has order 2, example #3 has order 3, and example #4 has order 2.
Here are a few examples of shapes that DO NOT have rotation symmetry.

(Non-example #1 - the coloring eliminates it from having rotational symmetry.)
(Non-example #2 - the numbers around the board eliminates it from having rotational symmetry.)
POINT SYMMETRY
Definition
Point Symmetry exists when a figure is built around a point such that every point in the figure has a matching point that is:
- the same distance from the central point
- but in the opposite direction.
A simple test to determine whether a figure has point symmetry is to turn it upside-down and see if it looks the same. A figure that has point symmetry is unchanged in appearance by a 180 degree rotation – all shapes that have point symmetry have rotational symmetry with order of 2.

You will notice that the point of rotation is a midpoint between every point and its image.
| TEACHER NOTE -- I included this chart because it is a part of the objective but personally I would want students to explore and determine these one their own. I would also include square, kite, and anything else I could find!! |
CONCEPT 2 - Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself.
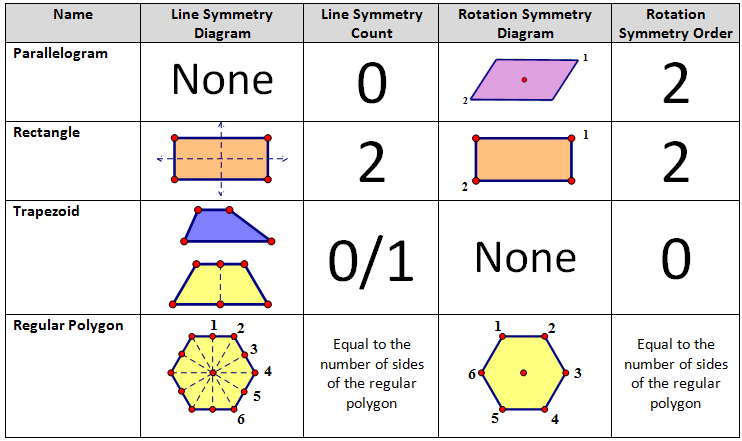
|










