CONCEPT 1 – The properties and characteristics of dilations.
 Dilation is the term that we use quite regularly in the English language to describe the enlarging or shrinking of our pupils. Pupils dilate either larger or smaller depending on the amount of light that enters the eye. This real world example helps us to understand the use of dilation in geometry as well – dilation is a transformation that produces an image that is the same shape as the pre-image but is a different size, either larger or smaller. Dilation is the term that we use quite regularly in the English language to describe the enlarging or shrinking of our pupils. Pupils dilate either larger or smaller depending on the amount of light that enters the eye. This real world example helps us to understand the use of dilation in geometry as well – dilation is a transformation that produces an image that is the same shape as the pre-image but is a different size, either larger or smaller.
When we make things bigger using dilation we refer to that as an expansion or enlargement whereas if we use a dilation to make something smaller we use the term contraction or reduction.

When the dilation is an enlargement, the scale factor is greater than 1. What this means is that if you have a scale factor of 3, or sometimes written as 1:3, the image is three times bigger proportionally to the pre-image.
When the dilation is a reduction, the scale factor is between 0 and 1. What this means is that if you have a scale factor of ½, or sometimes written as 2:1, that the image is half the size proportionally to the pre-image.
So what happens if the scale factor is 1? Nothing!! To multiply anything by 1 maintains the pre-image. It is like rotating a shape 360° - the shape is not altered in any way – it is an identity transformation.
So what actually happens when a shape is dilated?
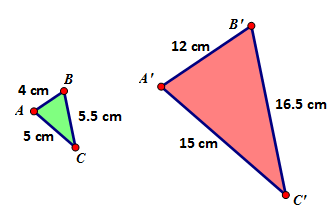
The length of each side of the image is equal to the length of the corresponding side of the pre-image multiplied by the scale factor,
A’B’ = k · AB, B’C’ = k · BC and A’C’ = k · AC.
This dilation has a scale factor of 1:3.
AB : A’B’ 4 : 12 1:3
BC : B’C’ 5.5 : 16.5 1:3
AC : A’C’ 5 : 15 1:3
|
 |
The distance from the center of the dilation to each point of the image is equal to the distance from the center of the dilation to each corresponding point of the pre-image figure times the scale factor,
OB’ = k · OB and OC’ = k · OC.
Scale Factor of 1:k
OB = y OB’ = ky y:ky 1:k
OC = x OC’ = kx x:kx 1:k |
 |
DEFINITION
A dilation with center O and a scale factor of k is a transformation that maps every point P in the plane to point P’ so that the following properties are true.
| The definition is an essential concept... slowdown and start with basic dilations - work with a single ray. It is upon a ray that they will gain the understanding of enlargement, reducation and direction of dilation. |

NOTATION
PROPERTIES
DILATION PROPERTIES - Dilation is NOT an isometric transformation so its properties differ from the ones we saw with reflection, rotation and translation. The following properties are preserved between the pre-image and its image when dilating:
- Angle measure (angles stay the same)
- Parallelism (things that were parallel are still parallel)
- Collinearity (points on a line, remain on the line)
- Distance IS NOT preserved!!!
After a dilation, the pre-image and image have the same shape but not the same size.
| Distance not being preserved but being proportional is of course the main focus of our study of dilations. Students need to understand what we mean by proportional. |
TRANSFORMATION PROPERTIES – The following properties are present in dilation:
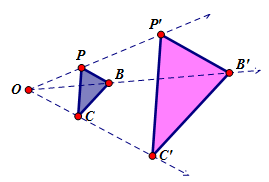 DISTANCES ARE DIFFERENT (PROPORTIONAL) – The distance points move during dilation depend on their distance from the center of dilation - points closer to the center of dilation will move a shorter distance than those farther away. In our example DISTANCES ARE DIFFERENT (PROPORTIONAL) – The distance points move during dilation depend on their distance from the center of dilation - points closer to the center of dilation will move a shorter distance than those farther away. In our example 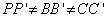 and point B is farther away from the center of dilation O than point P, thus and point B is farther away from the center of dilation O than point P, thus 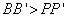 . .- ORIENTATION IS THE SAME – The orientation of the shape is maintained.
- SPECIAL POINTS – The center of dilation is an invariant point and does not move in a dilation. If the pre-image (P) = image (P’) after a dilation then point P was the center of dilation.
CONCEPT 2 - Verify experimentally the properties of dilations given by a center and a scale factor: a dilation takes a line passing through the center of dilation unchanged.
| Why would a dilation leave a line unchanged? Where would be the center of dilation if after a dilation the line maps onto itself? Of course on the line.... help students understand using the definition how points will be affected by the center of dilation. |

CONCEPT 3 - Verify experimentally the properties of dilations given by a center and a scale factor: a dilation takes a line not passing through the center of the dilation to a parallel line.
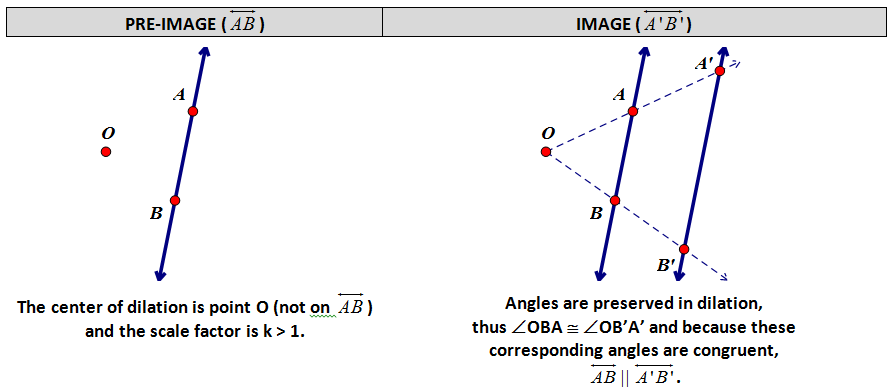
It is critical to understand that dilations create parallel lines between
ALL pre-image and image corresponding segments and lines.
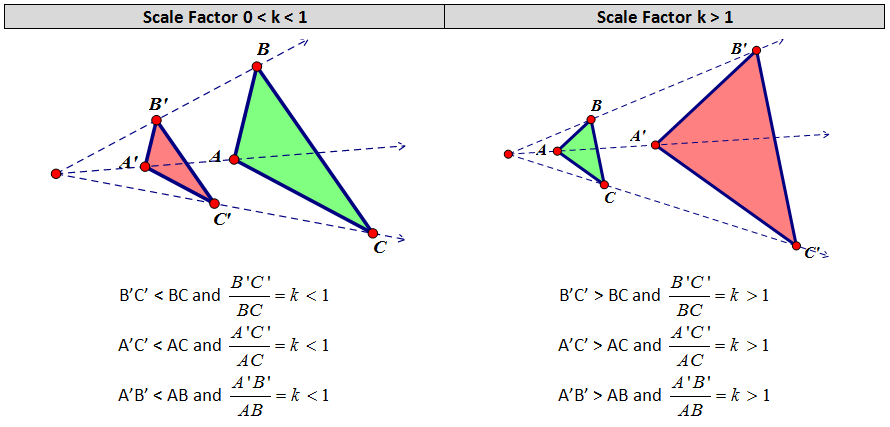
CONCEPT 4 - Verify experimentally the properties of dilations given by a center and a scale factor: the dilation of a line segment is longer or shorter in the ratio given by the scale factor.
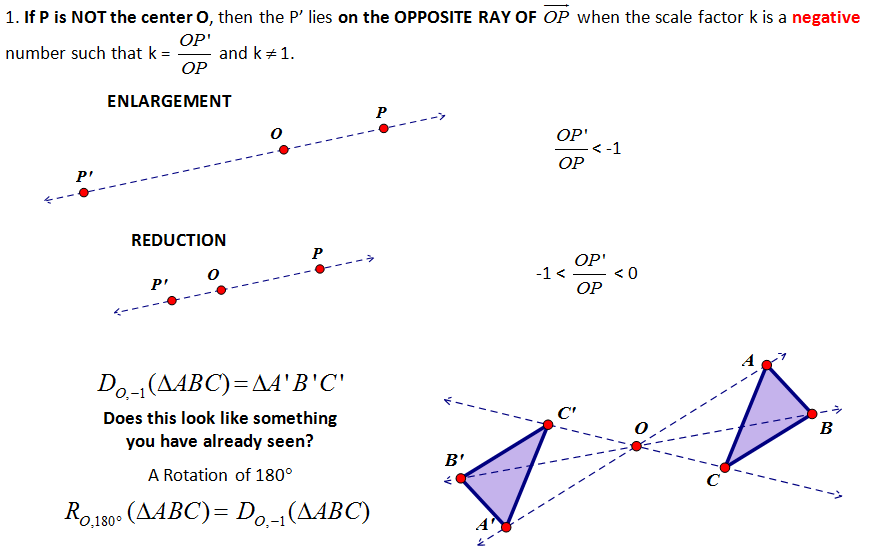
CONCEPT 5 – What happens when the scale factor is a negative number?
A dilation with center O and a scale factor of k is a transformation that maps every point P in the plane to point P’ so that the following properties are true.
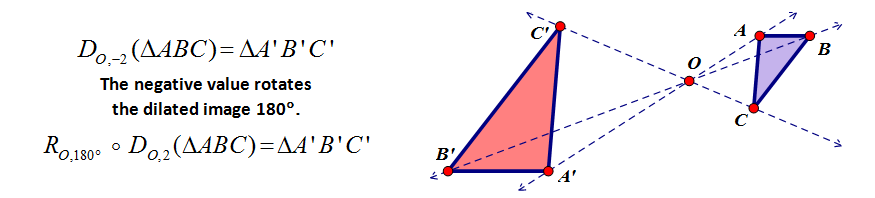
| This is a great connection - that a rotation of 180° is a dilation of -1. Why would that be? |
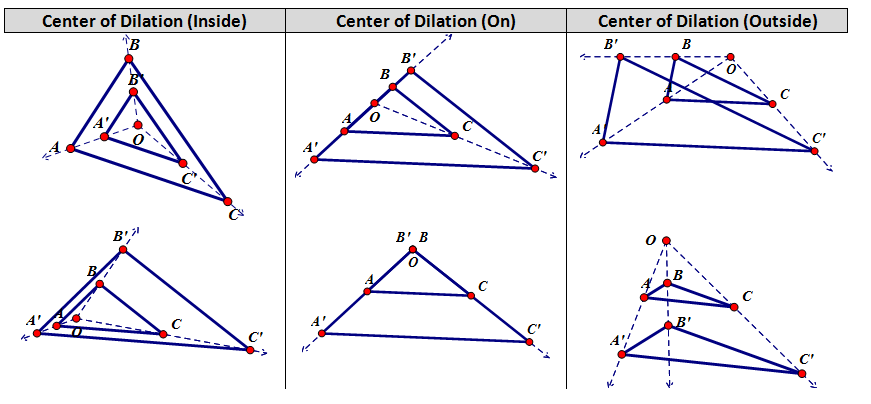
CONCEPT 6 – What happens when the center of dilation is in, on and out of a figure?
Three very distinct diagrams appear for these three situations.
CONCEPT 7 – The coordinate rule for dilation.
There is not much to discover here because the coordinate rule is provided in the definition,
We had already discovered this intuitively in G.CO.2 when we were investigating isometric and non-isometric transformations. We found out that if you multiply one or two variables by a value other than 1 or -1 you are no longer isometric. We also established a difference between the dilation and the stretch. A dilation must have the same value multiplied to both variables, whereas the stretch has different values.

It is obvious that for a dilation to maintain its proportionality of sides,
the two variables must be multiplied by a constant value, k, known as the scale factor.
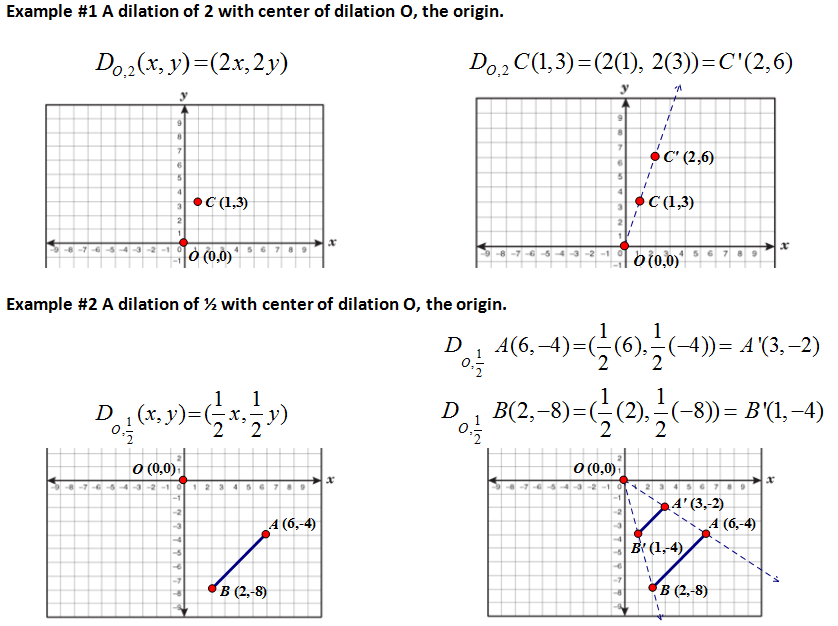
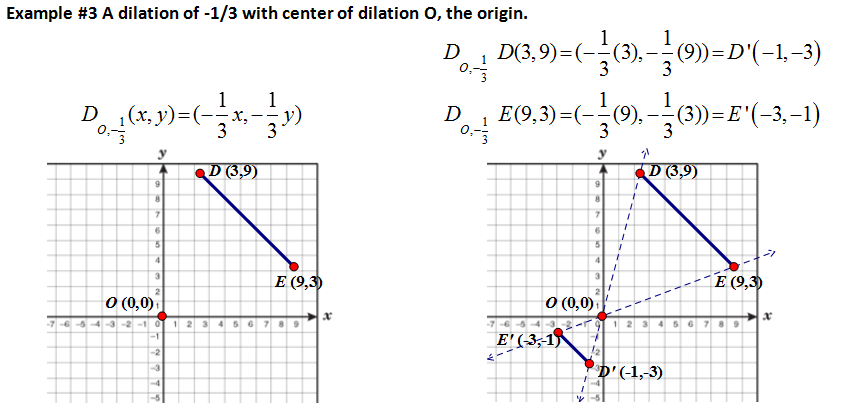
Examples using the coordinate rule of dilation when the center of dilation is the origin.
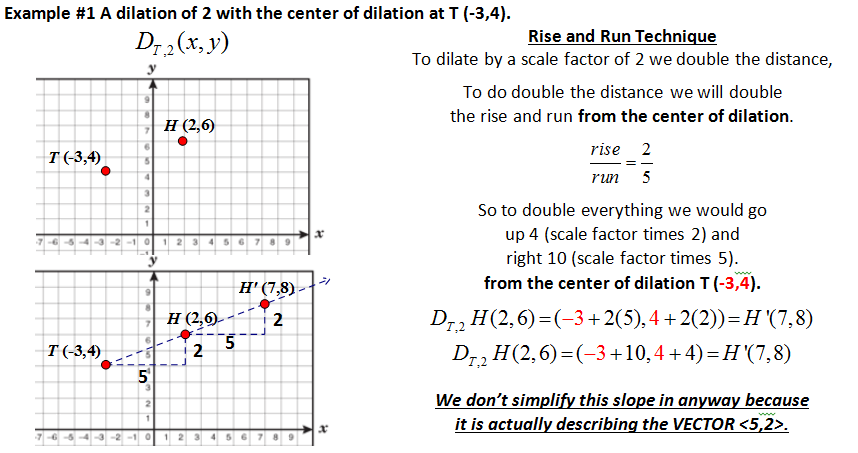
Examples using the coordinate rule of dilation when the center of dilation is NOT the origin.
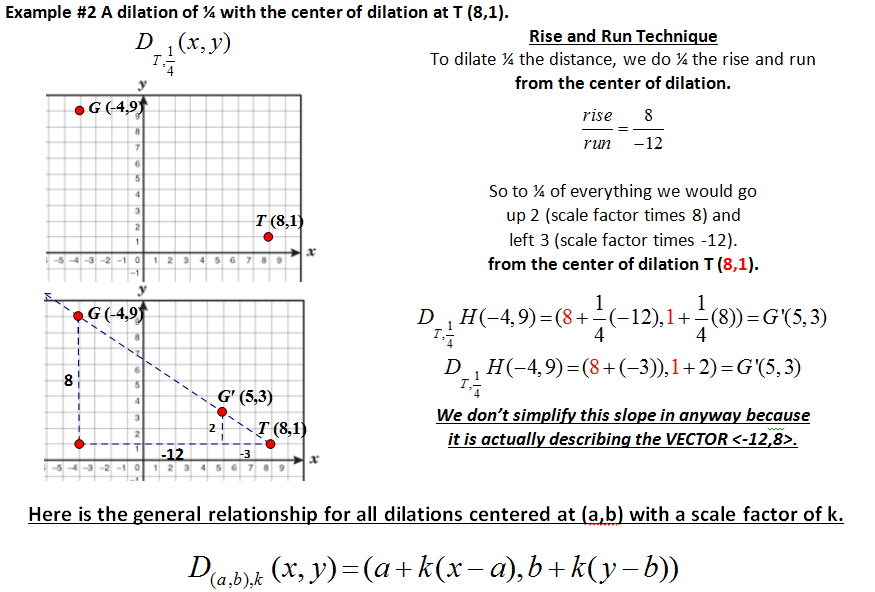
| This is a nice connection to another objective - partitioning a line segment. This will be a great preparation for that later in the year. |
|


 Dilation is the term that we use quite regularly in the English language to describe the enlarging or shrinking of our pupils. Pupils dilate either larger or smaller depending on the amount of light that enters the eye. This real world example helps us to understand the use of dilation in geometry as well – dilation is a transformation that produces an image that is the same shape as the pre-image but is a different size, either larger or smaller.
Dilation is the term that we use quite regularly in the English language to describe the enlarging or shrinking of our pupils. Pupils dilate either larger or smaller depending on the amount of light that enters the eye. This real world example helps us to understand the use of dilation in geometry as well – dilation is a transformation that produces an image that is the same shape as the pre-image but is a different size, either larger or smaller.




 DISTANCES ARE DIFFERENT (PROPORTIONAL) – The distance points move during dilation depend on their distance from the center of dilation - points closer to the center of dilation will move a shorter distance than those farther away. In our example
DISTANCES ARE DIFFERENT (PROPORTIONAL) – The distance points move during dilation depend on their distance from the center of dilation - points closer to the center of dilation will move a shorter distance than those farther away. In our example 









