| |
CONCEPT 1 – Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.
In G.CO.2 we defined a transformation to be a one to one correspondence between the points of the pre-image and the points of the image and then narrowed that definition down to an isometric transformation as a transformation that preserves the distances and angles between the pre-image and image. We will now create another classification of transformations, the similarity transformations.
A similarity transformation is a transformation in which the image has the same shape as the pre-image. Specifically, the similarity transformations are the isometric transformations (reflection, rotation, translation) and dilation as well. The Venn diagram below displays how all these are related to each other.
| Similarity transformations is a new concept.... It is simply the isometric transformations and dilations. The isometric transformations are a dilation of scale factor 1 and so they preserve the shape as well as dilations. |
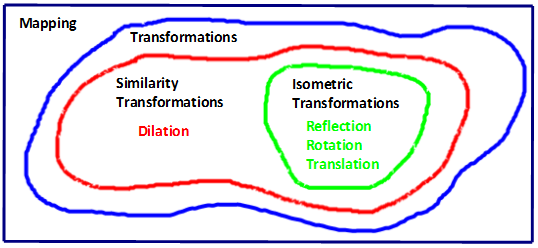
All transformations are mappings.
All similarity transformations are transformations.
All isometric transformations are similarity transformations.
|
 |
From this Venn diagram we learn that congruence is a subset of similarity. Congruence requires both same shape and same size whereas similarity only requires same shape.
Definition of Similarity
Two figures are similar if and only if one can be obtained from the other
by a single or sequence of similarity transformations.
Notation
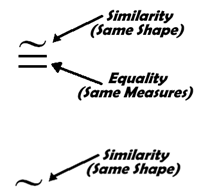
If you remember when we introduced the congruence symbol, we presented you with this diagram. The congruence relationship has two facets to it, same measure (equal corresponding lengths) and same shape (equal corresponding angles) thus the symbol includes both parts of that relationship.
When working with similarity, where only the same shape is required, we see a slight change to the symbol; we only use the ‘squiggle’. |
 |
Writing Similarity Statements
So if we are to write a similarity statement for ΔABC and its dilated image, ΔDEF. We know these two triangles are similar because the similarity transformation of dilation maps ΔABC onto ΔDEF. As we did with congruence we correlate the corresponding angles and sides in the name.
|
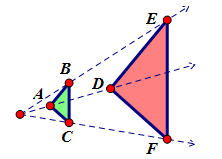 |
If ΔABC ~ ΔDEF then;

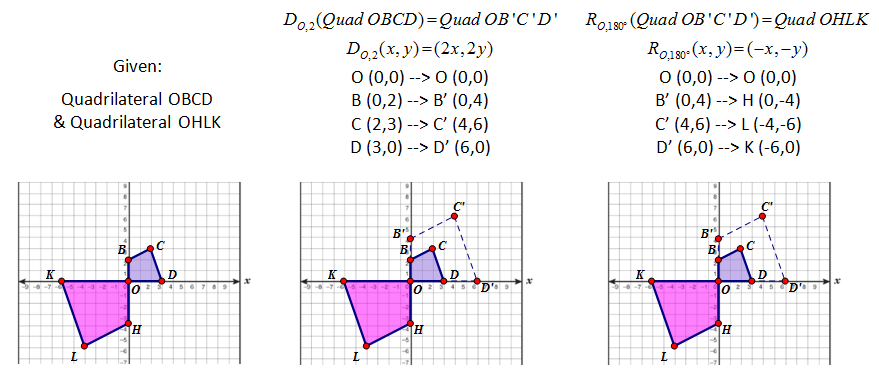
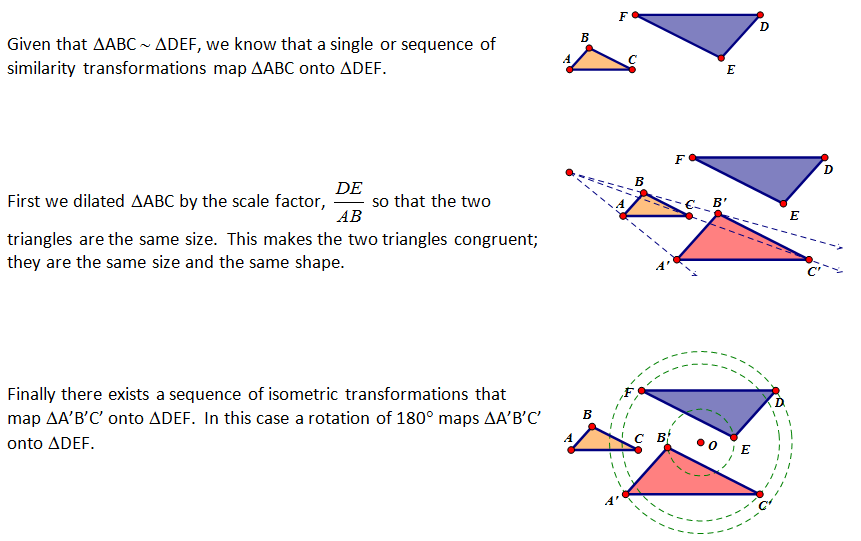
| To establish similarity we need to map a figure onto another using only similarity transformations and if that is possible, they those two figures are similar. This can be done nicely on a grid as demonstrated below because students can apply their coordinate rules to obtain exactness in the mapping. |
Establishing Similarity through Similarity Transformations
|








