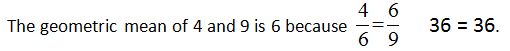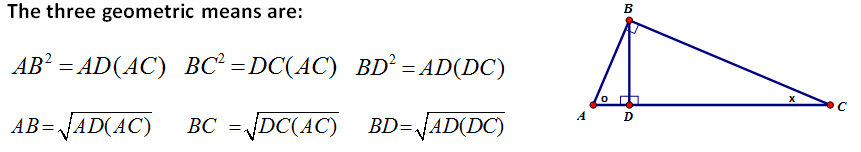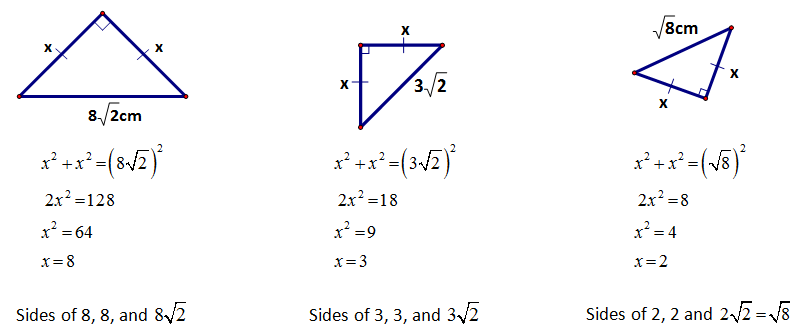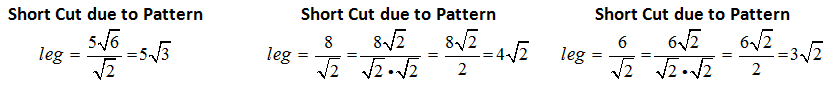CONCEPT 1 – Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures – Geometric Mean.
Geometric mean…..?
Is that the same mean referred to when we say MEAN, MEDIAN AND MODE? NO!! That mean is actually called the Arithmetic Mean. The Arithmetic mean of n numbers is the sum of values of the numbers divided by n. The Arithmetic Mean determines the ‘average’ number of the group.
Geometry has its own mean and is much different than the Arithmetic Mean. The Geometric Mean of two numbers, a and b, is the unique number x such that:
This is quite a special situation, where x is used as denominator in one ratio and as a numerator in the other and yet BOTH RATIOS EQUAL EACH OTHER. Let’s look at an example of this special situation.
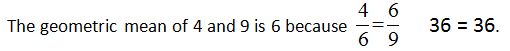
Let’s find the geometric mean of a few different values.

So the question becomes…. What does this have to do with geometry? Great question!! This unique proportion appears in a special type of triangle and it has a lot to do with similarity.
| When we take the square root we get both the positive and negatives values and we tend to drop the negative value because the geometric mean represents a distance. |


| Geometric mean has always been difficult for students to understand. The overlapping triangles and the double use of certain sides is difficult to visualize. Have students diagram the two triangles separated from each other as I will do below. It helps to relate the two triangles and their ratios. |

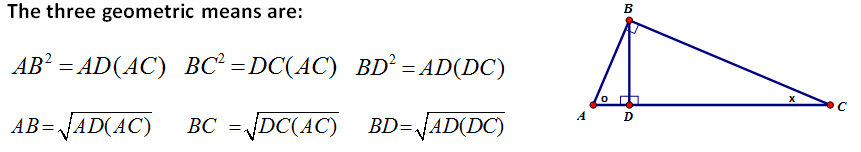
CONCEPT 2 – Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures – Special Right Triangles.
There are two triangles that receive ‘special’ attention because of the specific geometric forms. These two triangles both come from regular polygons. The side ratios and angle measures found in these ‘special’ triangles get used all throughout mathematics and form the basis for ‘exact’ values for angles.
THE 45° - 45° - 90° TRIANGLE (RIGHT ISOSCELES)
The right isosceles is easily formed by drawing one of the diagonals of a square. By the properties that we discovered in G.CO.11 we know that the diagonals of a square (or a Rhombus) will be angle bisectors. Thus, the diagonal will divide the 90° angle into two 45° angles.
Because the Right Isosceles is formed from the square, we know that two of the sides must congruent and that the base angles must be equal (45°each). Let us now look at the side relationships. |
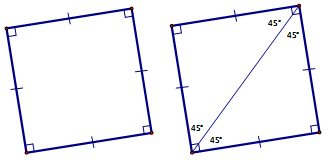 |


These examples help us to see a pattern with the three sides of a RIGHT ISOSCELES (45°, 45°, 90°) triangle.

Knowing this relationship we also solve for the legs of the right isosceles, if we know the hypotenuse.
Dividing by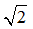 is always difficult for students to do. Most students think they are simply dropping the is always difficult for students to do. Most students think they are simply dropping the 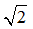 off and not dividing off and not dividing 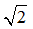 . If they percieve this as dropping instead of dividing they will not be able to do other values on the hypotenuse. . If they percieve this as dropping instead of dividing they will not be able to do other values on the hypotenuse. |
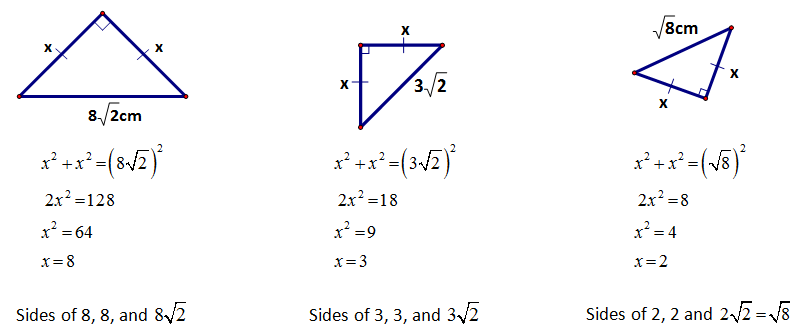

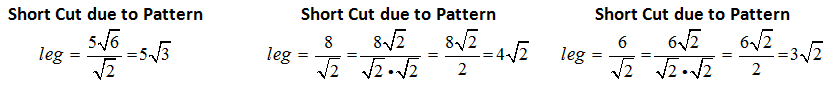
THE 30° - 60° - 90° TRIANGLE
| The 30°- 60° - 90° triangle is formed when the perpendicular bisector of a side of an equilateral triangle is drawn. The perpendicular bisector divides that side into two equal parts while also bisecting the opposite angle of 60° into two equal angles of 30°. |
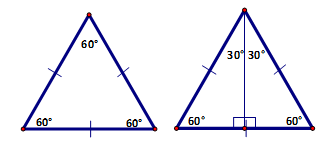 |
Because all three sides were congruent to start with, the side that was bisected is exactly half of the hypotenuse. This relationship is quite easy to remember, so we will focus on the relationship these two sides have with the other leg. |
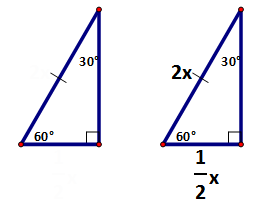 |
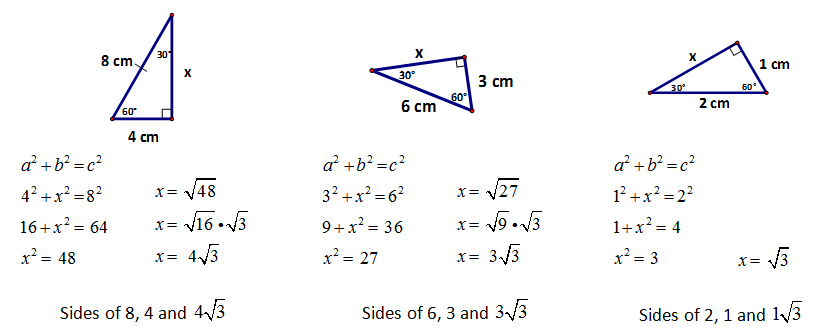

These examples help us to see a pattern with the three sides of a 30°, 60°, 90° triangle.
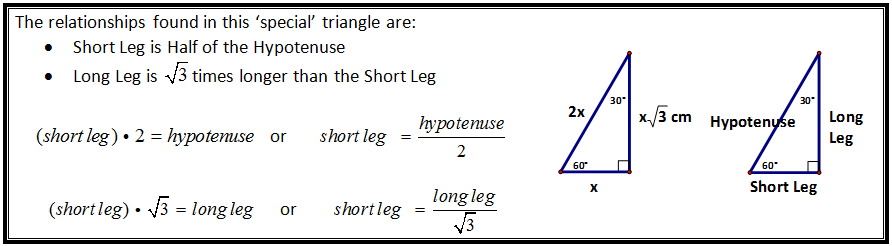
Knowing this relationship we also solve for the legs of the right isosceles, if we know the hypotenuse.

Again the division is the most difficult. Dividing by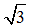 is difficult for students becausethey off perceive what is going on is to 'dropping' off the is difficult for students becausethey off perceive what is going on is to 'dropping' off the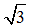 instead of dividing. instead of dividing. |

Why does the size of these two triangles not alter these side relationships?
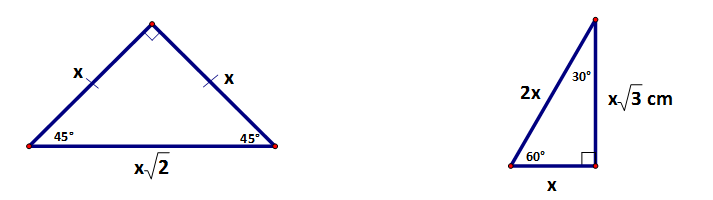
The answer is very simple…. SIMILARITY
All 45° - 45° - 90° are similar (by AA) and so the sides will maintain these proportional relationships.
All 30° - 60° - 90° are similar (by AA) and so the sides will maintain these proportional relationships.
At the heart of special right triangles is similarity.
|