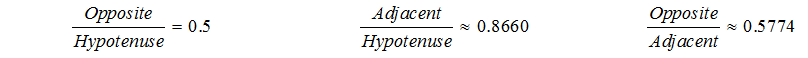CONCEPT 1 – Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.

In G.SRT.5 we discussed that all 45° - 45° - 90° right isosceles triangles have the same relationships of its sides no matter how large or small the triangle is.  These ratio relationships are unchanging due to the similarity of the triangles.  Similarity preserves the angle measures and maintains the sides’ proportionality. 

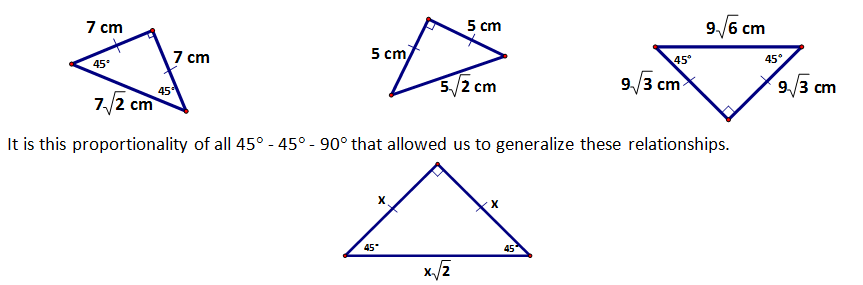
The ratios within the triangle such as the leg to the hypotenuse or the leg to the leg are fixed values because they would remain proportional no matter the size of the triangle.  If we calculated them we would find that:

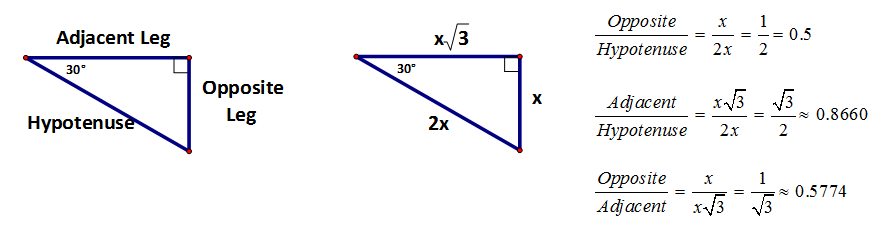
When looking at ratios within the triangle we need to name the sides so that we aren’t confused by which side or leg that we are referring to.  When we label sides it will always be based on a reference angle.  In the previous example we didn’t have to discuss this because the two reference angles were the same.

The hypotenuse will always be opposite the right angle (the longest side).
The opposite leg will always be the side of the triangle that does not form the reference angle.
The adjacent leg will always be the non-hypotenuse side that forms the reference angle.

So if we look at the ratios of the sides of a 30° - 60° - 90° triangle we need to identify which angle we are referring to.  In the below example we will refer to the sides based on the reference angle of 30°.

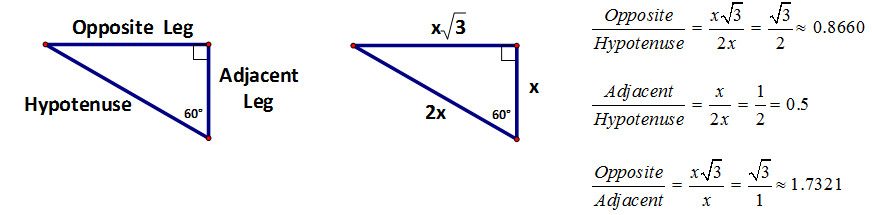
In this next example, we will use the 60° angle as our reference angle. Notice how the Opposite and Adjacent sides differ due to the new reference angle location.  The hypotenuse will always stay stationary.

What we begin to recognize is that the 30° right triangle has three fixed ratios:

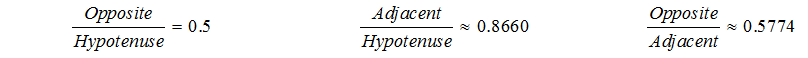
We also realize that all 60° right triangles have three fixed ratios:

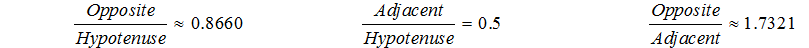
We can also now extrapolate this concept to any reference angle in a right triangle….  That there will be three ratios that exist for all of those as well.  It is this concept that is the basis for TRIGONOMETRY.

TRIGONOMETRY (Triangle Measure) allows us to link angle size in right triangles to side proportionality.  If we know the reference angle in a right triangle, then there are three fixed ratios of its sides.  The converse is also true, if we know the ratio of two sides of a right triangle then there exist one reference angle that has this ratio.  Trigonometry connects angle measure to side measure, thus it is a very powerful piece of mathematics.

These three ratios that we have established have names:

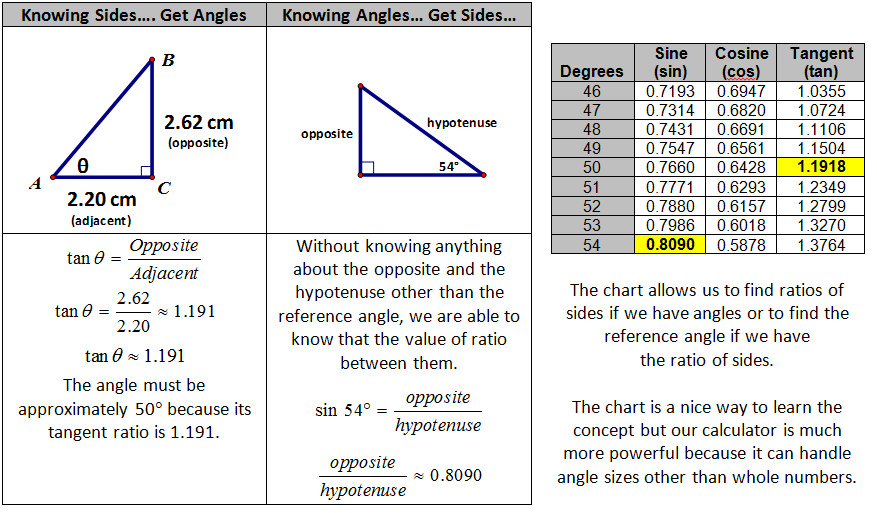
Below is a table of the three ratios (Sine, Cosine & Tangent) for all whole number value angles from 0° to 90°.  I highlighted the three reference angles that we just did.  This table is a clear demonstration of how angles relate to side ratios and side ratios relate to angles.

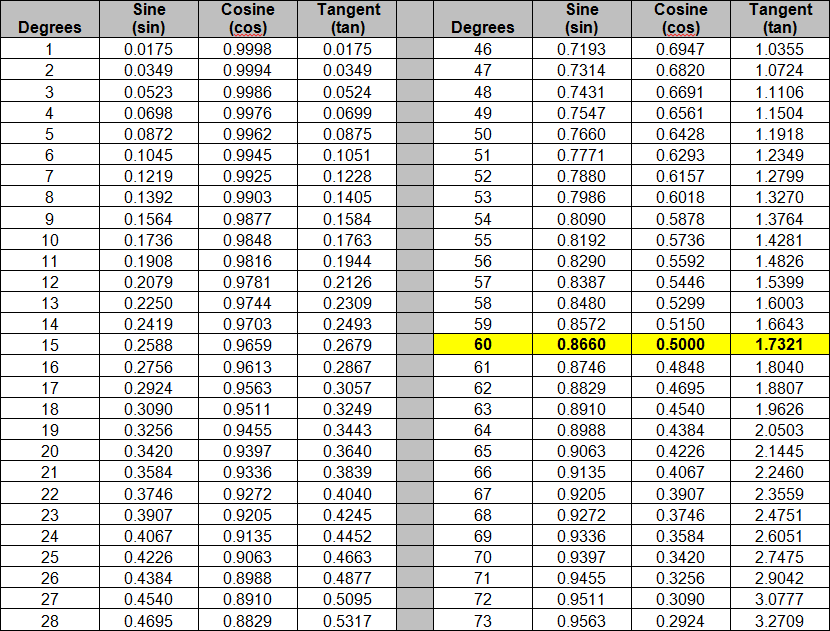
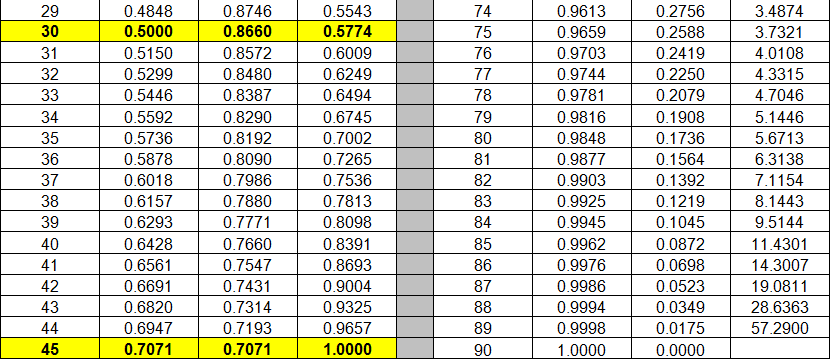
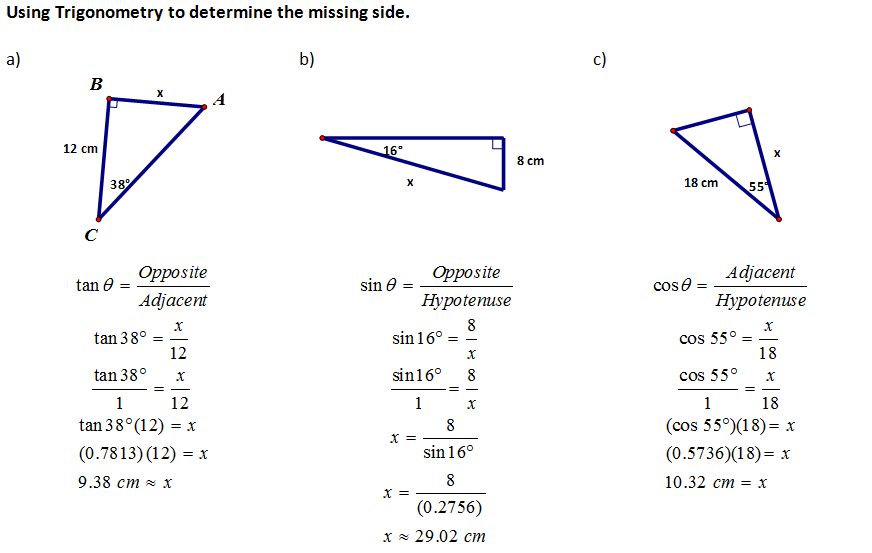
Lets look at how trigonometry helps us discover information about triangles.

I have clipped a bit of the table to demonstrate the power of these numbers.