CONCEPT 1 – Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. *(Modeling Standard)
In this objective we apply the principles that we have learned concerning similarity, trigonometry and the Pythagorean Theorem to solve ‘real’ world problems. While we call them real world problems many of them have been greatly simplified so that the mathematics at this level can be applied. Real world problems have many variables and are often too complex to approach with this simple level of mathematics but as students’ progress through mathematics we add more detail to the problems making them ‘more real’. At this stage we want them to gain proficiency in the skill within a context to see where these mathematical tools apply.
We call these problems real world while students call them word problems. Yes that is often true… Real world problems do come with context and so yes they look and feel different than the standard symbol based problems that we often do. It also means that we need to gain proficiency with language as well as mathematics to succeed with these types of problems. Most of these notes will be discussing the context of these problems and the translation of word to mathematics and not the solving of them. That skill was discussed in an earlier objective. Let me start with how we refer to angles.
THE ANGLE OF ELEVATION
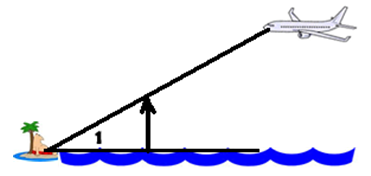
To elevate is the move in an upward direction. Thus the angle of elevation is an upward angle from the horizon. The angle of elevation is the reference angle from the position in an upward direction from the horizon.
The stranded person on the island looks up
to the plane at an ANGLE OF ELEVATION. |
|
 |
Very few students struggle with this concept – The name and the placement seem to come easily. This is not true concerning the next angle, many students struggle with its placement and understanding.
THE ANGLE OF DEPRESSION
To be depressed is to be down, thus the angle of depression is the reference angle from the position in a downward direction from the horizon. Sound simple like the angle of elevation but it isn’t quite as easy.

In example #1, the angle of depression (1) has been placed correctly, as the angle from the airplanes’ horizon looking down. In example #2, the most common error has taken place; the angle of depression (1) was PLACED IN THE WRONG LOCATION. Student’s make this error because no horizon has been drawn and so they see this as the only angle from that reference point. Finally, in example #3, the angle of depression (1) has been correctly drawn and located - placing it from the horizon down.
I also want to discuss some of the CLASSIC environments of trigonometry and Pythagorean problems and their particular terminology.
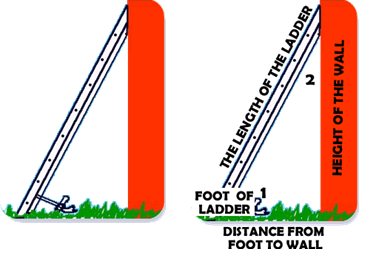 |
The leaning ladder or pole is a common trigonometry problem because of the natural right angle formed between the wall and the ground. The ladder or pole becomes the hypotenuse of the triangle. A word that gets used that may be new to the student is the FOOT of the ladder – the foot of a ladder is the bottom of the ladder that is placed on the ground. The two complement angles are often referred to as (1) the angle formed between the ladder and the ground and (2) the angle formed between the ladder and the wall.
Assumptions Made: That the ground and the wall always make a right angle. |
THE KITE PROBLEM

The kite problem is another classic!! The length of the string of course is the hypotenuse. The perpendicular distance from the kite to the ground is the height or altitude of the kite and then other leg gets referred to as the horizontal or ground distance. The only angle I ever see used here is (1) the angle of elevation from the boy to the kite.
Assumptions Made: Lots here… We assume the string is tight, we assume that he is flying the string from his big toe and not his hand. We can fly the kite from his hand but it would add an additional layer of explaining that isn’t often provided in the early trigonometry problems.
THE GUY WIRE
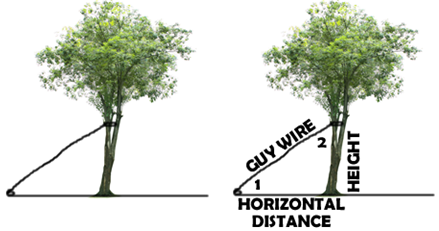 |
A guy wire is a wire that is used as a brace to stabilize something. They are used on young trees to help stabilize them in windy or stormy conditions so that they don’t pull their roots out of the ground. They are also used to stabilize antennas, satellite dishes, towers, etc…. they are basically brace supports. In these problems the tree and the ground form the right angle, and the wire or brace becomes the hypotenuse. The other descriptions are similar to other problems already discussed.
Assumptions Made: That the ground and tree make a right angle and that the wire or brace is straight. |
THE SHADOW
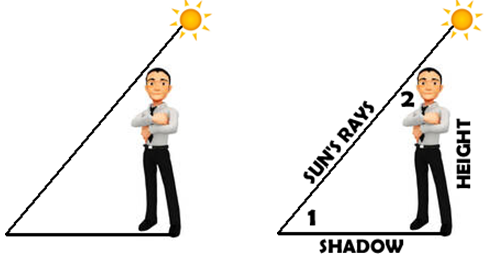 |
First of all shadows are ALWAYS ON THE GROUND. Too often shadows are viewed by students as the hypotenuse – that is wrong. We don’t often calculate for the sun’s rays because it isn’t something that makes sense to measure, so we are usually finding the man’s height or his shadow or (1) the angle formed by the sun’s rays and the ground. The other angle (2) would be the angle formed by the sun’s rays and the man.
Assumptions Made: That the man is standing straight up (perpendicular to the ground). We are also assuming that we have a way to measure the angle of the sun to the ground… I’m sure there are other assumptions here …… |
VIEWING SOMETHING
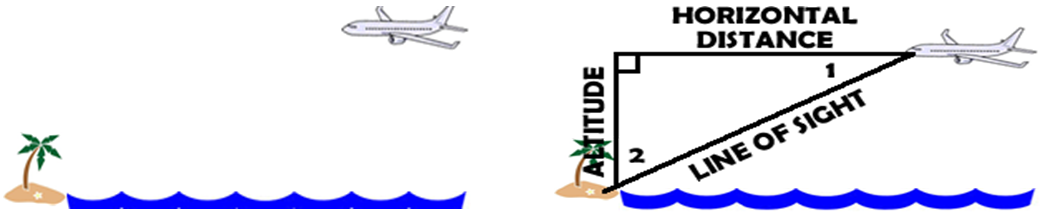
When viewing something we use the phrase, the line of sight, to refer to the distance from your position to the object that you are viewing. So in this case, the pilot spots the island and that distance is called his line of sight. Also in this case because the pilot is looking down from his horizon, the angle (1) that he is using is the angle of DEPRESSION from the pilot/plane to the island. Planes and objects in the sky often give their height by stating the ALTITUDE of the object.
Assumptions Made: I can’t think of any assumptions for this one, but I’m sure there are.
Finally I want to discuss two types of problems that increase the difficultly level a bit.
Level 2 Difficulty -- THE USE OF TWO TRIANGLES
The use of two triangles just simply means that you will solve for two different values to gain the final answer. Really this problem isn’t an increase of difficulty it is simply an increase on work. It often gains difficulty because it does require more contexts to explain what is going on.
Example Problem
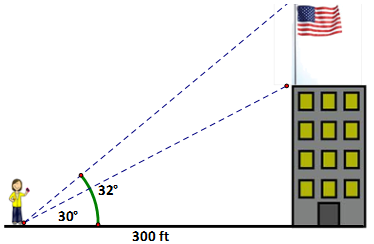
A flagpole is at the top of a building. 300 ft from the base of the building, the angle of elevation of the top of the pole is 32° and the angle of elevation of the bottom of the pole is 30°. Determine the length of the flagpole (to the nearest foot).
This problem looks quite complex because of the overlapping angles of elevation but really if we think through the problem we can simplify it by solving two different triangles. |
 |
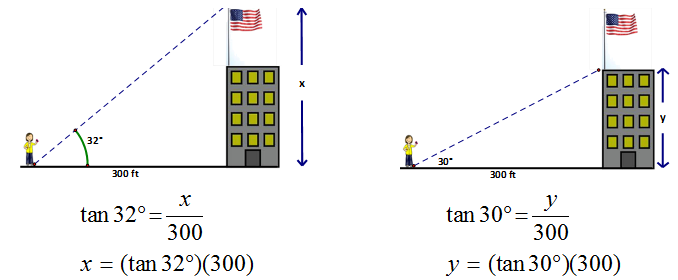
The way to get the height of just the flagpole would be to calculate the total height from ground to top of flag (x) and then calculate the distance from ground to the bottom of the flagpole and then subtract the two values.
x – y will give us the flagpole height,
187.46 – 173.21 = 14.25 ft |
|
 |
Not all two triangle problems work exactly like this… sometimes you add the values to get the answer, and other times you use one value to obtain the second value…. Ultimately though the concept is similar – these problems will require you to calculate two trigonometry problems to obtain one answer.
Level 3 Difficulty -- A SYSTEM OF EQUATIONS
In algebra 1 we learned how to solve two variables if we had two equations. This process was called solving a system of equations. We learned a few different ways to solve them; (1) by graphing, (2) by substitution, and finally (3) by elimination. We will look a trigonometry problem that will give us two equations and two variables and we will use substitution to solve it.
Example Problem
Sally and Jonathan are on either side of the tree and 40 ft apart. Sally sees the top of the tree at 42° and Jill sees the top of the steeple at 36°. How high is the tree (to the nearest foot)?
|
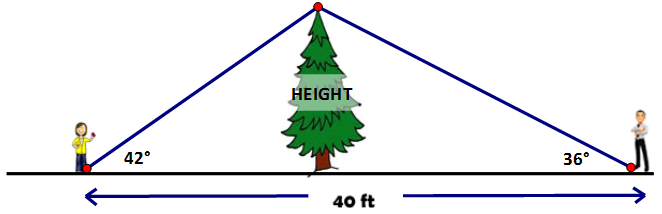 |
The first step is to break up the 40 ft, most students break the 40 ft into two groups of 20 but this can’t be because if the distances were equal then so would there angles (the tree would be the perpendicular bisector of an isosceles triangle) but the angles aren’t equal so neither will the distances.
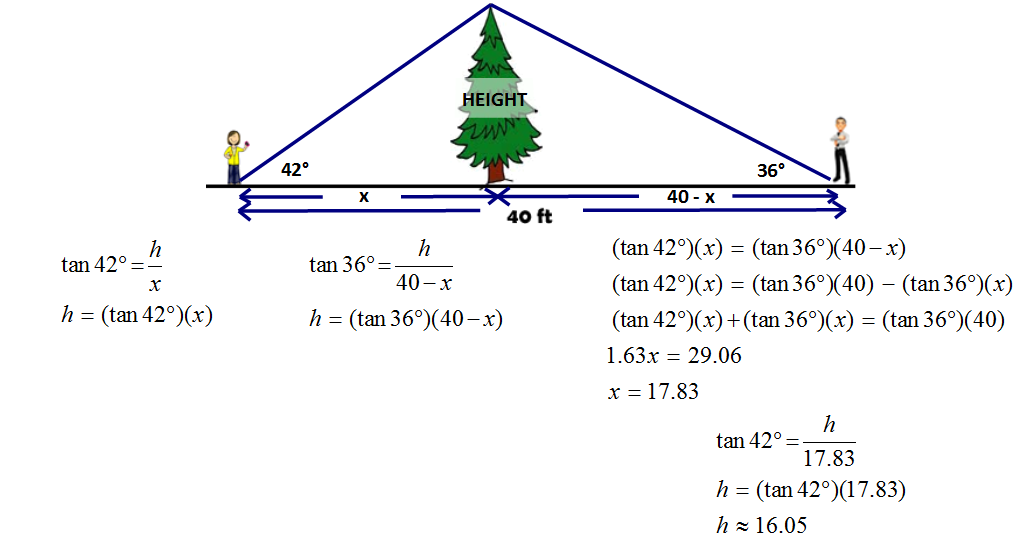
This is just one way to solve this problem, as mentioned earlier there are a number of algebraic techniques that could be applied here.
|












