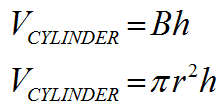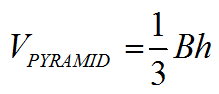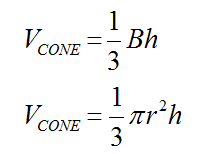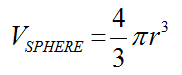| |
While objective G.GMD.A.1 was about determining the formulas for the solids, this objective focuses on the CALCULATIONS of the volume.
PRISM VOLUME CALCULATION
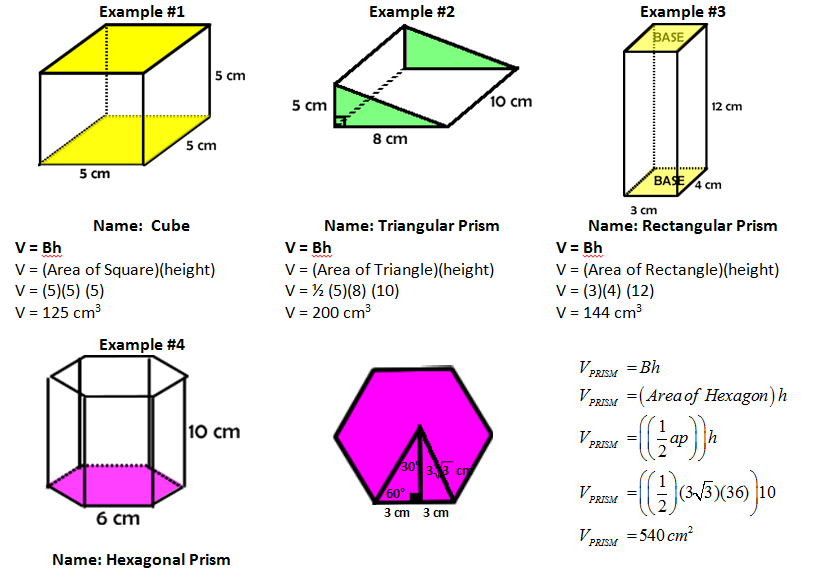
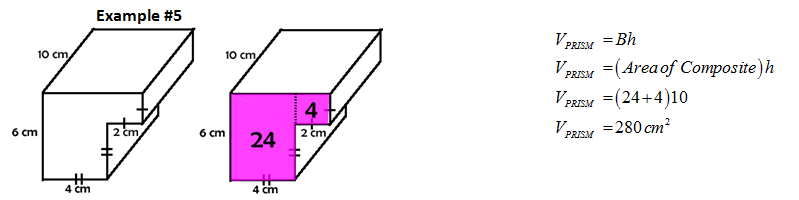
| The formula for the volume of a prism is quite simple. The capital B represents the AREA of the base. This sometimes confuses students because they might use the base of a triangle or the base of a trapezoid here instead of the AREA of the base. It is for this reason that this B has been capitalized to distinguish it different from b or b1. The height, h, refers to the height of the prism which is one of the lateral sides if it is a right prism. This too is sometimes confusing because bases will have heights as well. |
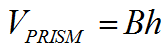 |
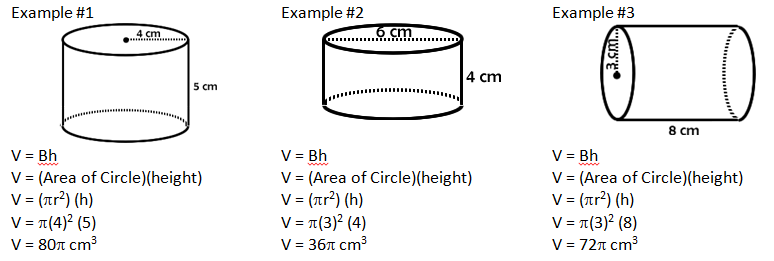
CYLINDER VOLUME CALCULATION
The formula for the volume of a cylinder is also quite simple. The capital B represents the AREA of the base but in this case the base will be a circle and so we can substitute in Πr2. The height, h, refers to the height of the cylinder which the perpendicular distance between the two circular bases. |
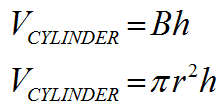 |
PYRAMID CALCULATION
The formula for the volume of a pyramid follows directly from the volume of a prism. The pyramid will always be 1/3 the volume of the prism with the same base and height. |
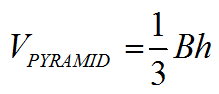 |
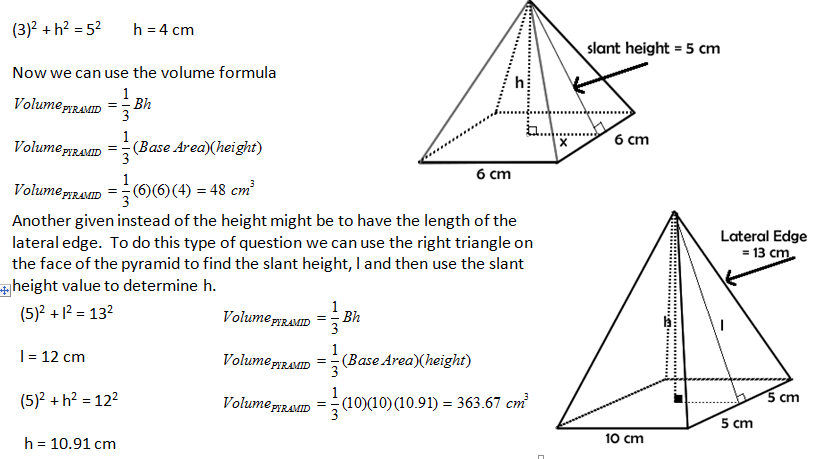
| Teacher Note: Two things happen once we get to pyraminds and cones..... First, we must emphasize to students the 1/3 relationship and second, how to use the Pythagorean Theorem to get the height from the slant height or the lateral edge. |

Sometimes with pyramids and cones the height of the solid is not given and we need to calculate it using the Pythagorean Theorem. In this example we have been given the slant height (l) – the height of the triangular face instead of the height of the pyramid. We are also missing the distance x but it is the apothem of the square and so it is half of the side, 3 cm.
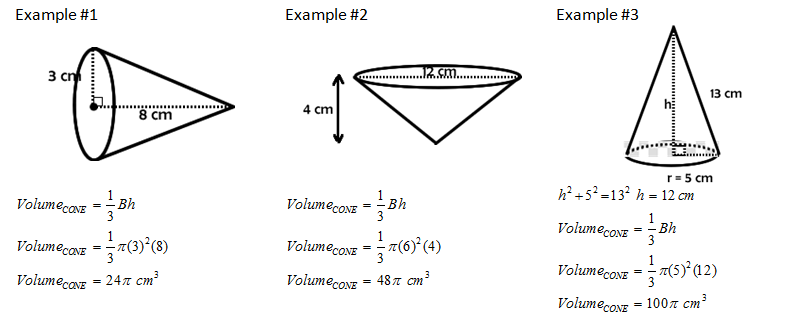
CONE CALCULATION
The formula for the volume of a cone follows directly from the volume of a cylinder. The cone will always be 1/3 the volume of the cylinder with the same base radius and height. |
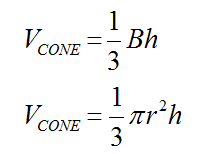 |
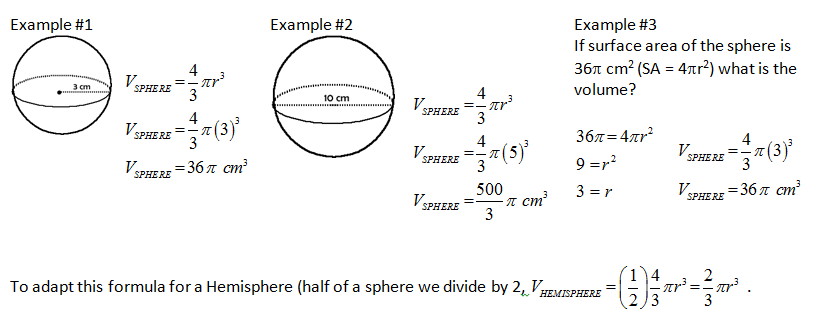
SPHERE CALCULATION
The formula for the volume of a sphere is a much more difficult one to visualize. The nice thing about this formula is that there is only one variable involved, the radius. The radius represents all three dimensions. |
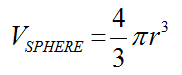 |
| Teacher Note: The sphere formula holds two challenges for our kids... the use of 4/3 and the fact the radius is cubed, not squared. These two things seem to hold kids back from what should be a single variable simple formula. |
|