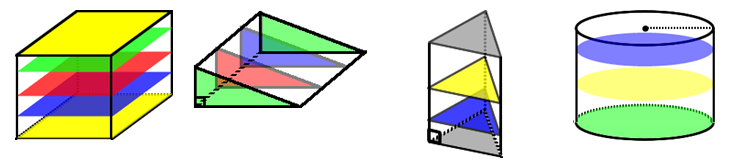
CONCEPT #1 -- IMPORTANCE OF CROSS SECTIONS

Cross sections of solids are an important part of understanding volume.  Notice that we used cross sections to conceptually understand the volume formulas for prisms and cylinders.  Base area times Height is a direct result of STACKING congruent cross sections on top of each other to ‘fill’ in the shape.  Below are a few visual examples of how cross sections are used to fill the shape and create volume.

Stacking of congruent cross sections on top of each other fills the space and creates volume.  Cavalieri also knew of the importance of cross sections when he compared the volume of two different solids.  Cavalieri’s principle states that:

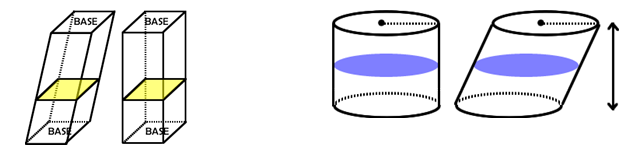
Using cross sections he was able to establish that two volumes were equal or not by matching the area of the cross sections.  It is this principle that allowed us to compare right and oblique prisms and cylinders to determine that indeed their volumes were the same.  As long as each cross section area matched and they had the same height then Cavalieri’s Principle helped us conclude the equality of volume.

We even used cross sections to approximate the relationship between prims and pyramids or between cylinders and cones.  To do this we again used cub cross sections. While these cross sections did not have equal area they did help us determine a relationship between the two volumes.  We found that the volume of the pyramid is 1/3 the volume of the prism with the same base and height.

So it is quite obvious that having an ability to see cross sections and how they relate to the solid is very important.  Volume relies heavily on the visualizing cross sections.  In all of the previous cases our cross sections were parallel to the base.  This of course was done on purpose to show how the volume is either congruent or proportional.  The other thing to notice about these parallel cross sections is that they were always the same shape, congruent or proportional, as the base.  Not all cross sections work this way.

CONCEPT #2 – VISUALIZING CROSS SECTIONS

When studying cross sections we want to look at not only the ones parallel to the base but also of the other possible types of cross sections.  For instance if we start with a cube, what are some of the possible cross sections (or cuts) that can be made.  To visualize this you need to be able to not only see the typical parallel cuts but many other types.

The question that arises when doing other cross section is what are all of the possible types of cross sections?  Could we get an equilateral triangle, a rectangle, a parallelogram, a scalene triangle, a hexagon or a decagon?   Through exploration students are able to investigate these different cross sections but ultimately they will find that the maximum number of sides of the cross section produced is the same as the number of faces of the solid.  So in the case of a cube, YES, a hexagon is possible but NO a decagon is not.

Exploring this in a two dimensional world is quite difficult and abstract for students.  It is hard to draw cross section of solids correctly.  I have not found the best way to do this….. cutting cheese cubes (expensive) --cutting Styrofoam cubes (messy and expensive) -- cutting play-doh (not very precise).  Ultimately I think the best way to explore cross sections is through technology.  There are a number of different cross section graphing programs on the web but SHODOR INTERACTIVE is my suggestion.

SHODOR INTERACTIVE   http://www.shodor.org/interactivate/activities/CrossSectionFlyer/   This cross sectional tool is amazing.  It allows you to not only freely alter the cross section you can also alter the characteristics of the solid.  This is a very powerful tool to use.   There are others that do similar things but nothing as easy to use as this one.   You can explore much more than just cubes and prisms.  This allows for cross sections of cones, cylinder, pyramids and prisms.

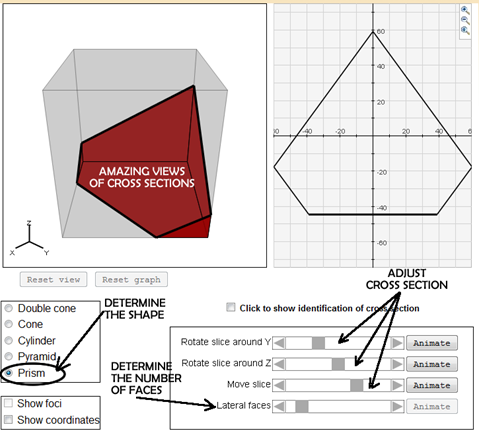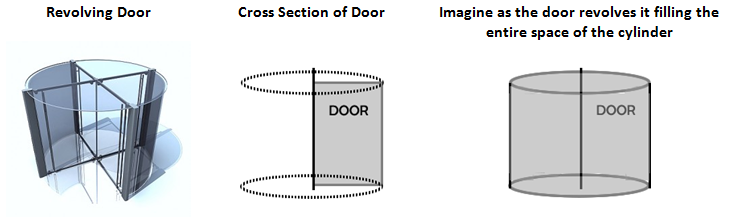
CONCEPT #3 – REVOLING 2-D SHAPES TO GET VOLUME

Instead of stacking congruent cross sections to form the volume of a solid another technique is to rotate is about an axis.  Thinking about a revolving door and how it swings (rotates) about the center creating a cylindrical shape.

So a different way to fill space and create volume is to rotate figures (2-D shapes) about an axis and in doing so fill space and create volume.  This technique gets used quite a bit in higher mathematics to determine the volume of a shape.  In calculus, we find ourselves finding the area under the curve for all kinds of different shapes.  This is great preparation for these ideas.