| |
 CONCEPT 1 – The Equation of a circle
The invention of Cartesian coordinates in the 17th century by René Descartes altered mathematics greatly. It provided a systematic way to connect Euclidean geometry to algebra. Using the Cartesian plane (also known as the coordinate plane) geometric shapes of all kinds could be described as an equation – an algebraic equation involving the coordinates of the points lying on the shape. For example, a circle with a radius 7 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 49.
Cartesian coordinates are the foundation of analytic geometry and provide enlightening geometric interpretations for many other branches of mathematics such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory, and more.
A group of curves often analyzed using the Cartesian plane are the conic sections. The conic sections refer to the cross sections of the cone or double cone. The conic sections are the ellipse, circle, parabola, and hyperbola. A circle cross section is formed when you cut a cone parallel to its circular base. In this objective we will analyze circles and their algebraic equations.
|
 |
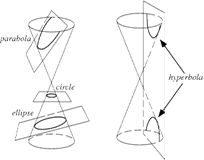The circle is defined as the locus (set) of points equidistant from a given point, called the center. When we apply this definition to the coordinate plane we realize that the Pythagorean Theorem will help us greatly because of its ability to calculate the distance of a segment. Actually the Pythagorean Theorem takes on a new name when we move from the general plane to the coordinate plane, we call it the distance formula. Many students use these two relationships regularly and never realize that they are actually the same relationship.
| Teacher Note: The connection between the Pythagorean Theorem and the Equation of a Circle is a great connection. Students need to derive this formula themselves. Start by doing the first this one with them (center at origin) and then have them do the next one on their own (center at (h,k)). |
So is a circle centered at the origin with a radius of 3 cm and x2 + y2 = 64 is a circle centered at the origin with a radius of 8 cm. One of the errors that students often make is that they do not square root the value when listing the radius value. Now not all circles are centered at the origin - wouldn’t that be easy. Let us do this exercise again except that we will use a generic center, C (h,k).
| Teacher Note: As mentioned above the radius value gives students the greatest issue... they use the value as is for the radius instead of taking the square root of the value. |
CONCEPT 2 – Completing the Square
| Teacher Note: It definately pays off to spending time on binomial multiplication patterns before beginning completing the square. It helps them see the pattern and hopefully understand where the relationships come from. |
|
