CONCEPT 1 – The Definition of a Parabola
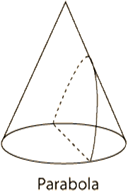
As mentioned in the previous objective the conic sections represent the curves that can be found from the cross sections of the cone or double cone – the circle, parabola, ellipse, and hyperbola. A parabolic curve can be found by cutting into the cone so that it passes through the lateral face and the base.
While most students could tell you the basic definition of a circle before entering geometry, very few could tell you the definition of a parabola. |
 |
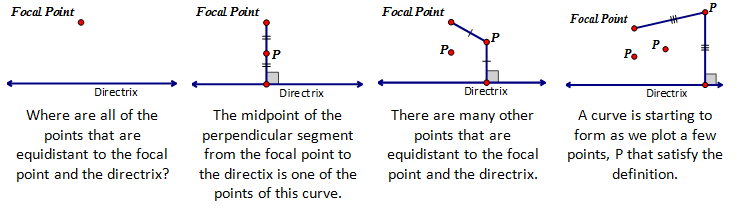
A parabola is the locus (set) of points that are equidistant from a fixed point,
called the focus, and a straight line, called the directrix.
|
|
The definition of a parabola even after hearing it is still quite illusive to students because it is very hard to visualize why this would create that particular curve. Breaking down the definition geometrically is very important to helping them understand it.
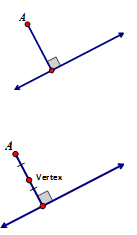
It is important to remember that the distance from a fixed point to a line is found in the perpendicular distance. The shortest distance from any point to a line is the perpendicular distance.
In an attempt to visualize the points that satisfy this definition most students see the midpoint of the perpendicular distance from the focal point to the directrix. This is only one point of the parabola but actually it is a very important one. It is the vertex of the parabola. The vertex will either be the minimum or maximum value of the parabola depending on its orientation in the plane.
|
 |
| Teacher Note: This relationship is brand new to students and the definition does not easily allow the student to determine the curve formed from it. Spend time developing the curve using the definition. It will help later when working with focal points and directrix. |
CONCEPT 2 – The Construction of a Parabola
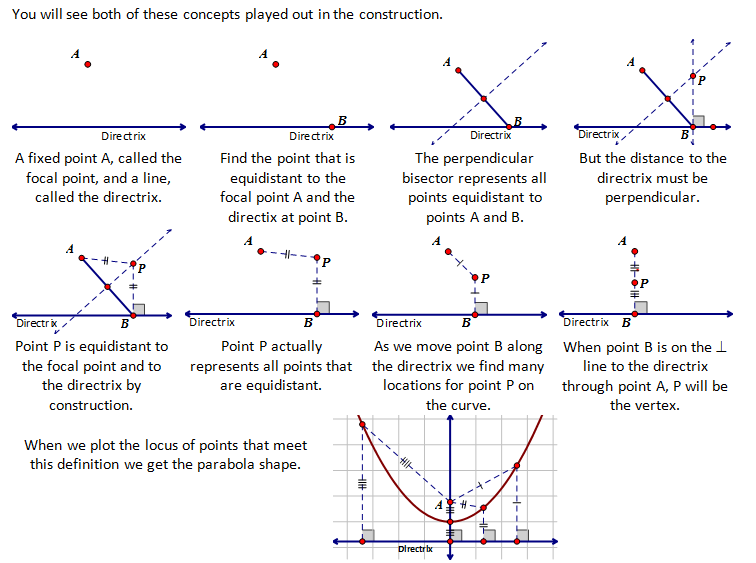
Before going to the coordinate plane to derive an equation for the parabola, I think it is important to first be able to construct it. The physical construction of the parabola will help us to understand how to approach the equation on the coordinate plane.
I want to emphasize two important concepts in the definition.
(1) For a point to be equidistant to two points it must be on the perpendicular bisector of those two points.
(2) If one of the distances is a distance to a line, then it will be a perpendicular distance to that line.
You will see both of these concepts played out in the construction.
CONCEPT 3 – The Equation of a Parabola
To arrive at the equation for the parabola we use its definition. To set this up we generate coordinates that represent these relationships. For simplicity we will use the origin (0,0) as the vertex. This creates a focal point that is directly above it, A(0,p) and a directrix that is the same distance from the vertex but in the opposite direction, y = -p. Traditionally the distance to the focal point from the vertex is labelled as p.
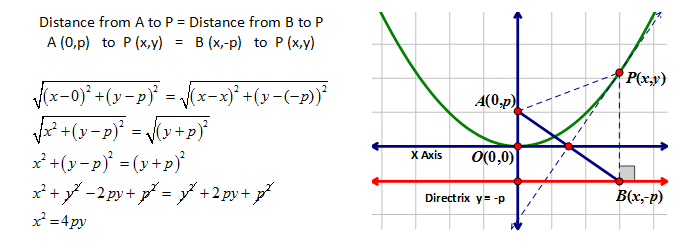
| Teacher Note: For simplicity, all parabolas dealt with at this level have the orgin as their vertex. You can expand this if you feel it appropriate. |
A couple of things to notice in our derivation of this equation:
(1) We arranged it so that the vertex of the parabola would be at the origin (0,0). It is the exact midpoint of the perpendicular distance from the focal point A (0,p) and the directrix, y = -p. In this objective we will only work with parabolas with a vertex at the origin.
(2) The value of p represents the distance from the vertex to the focal point and the distance from the vertex to the directrix in the opposite direction.

CONCEPT 4 – Understanding the Equation of a Parabola
As with all equations the x and y values represent the x and y coordinates of the points that lie on this curve. This leaves the p value as the only thing to discuss. The value of p, the distance from the vertex to the focal point, greatly alters the shape of the parabola. We just learned that the positive or negative orientation of p determines the direction that it opens. Below we will see that the size of p will also alter the parabola.
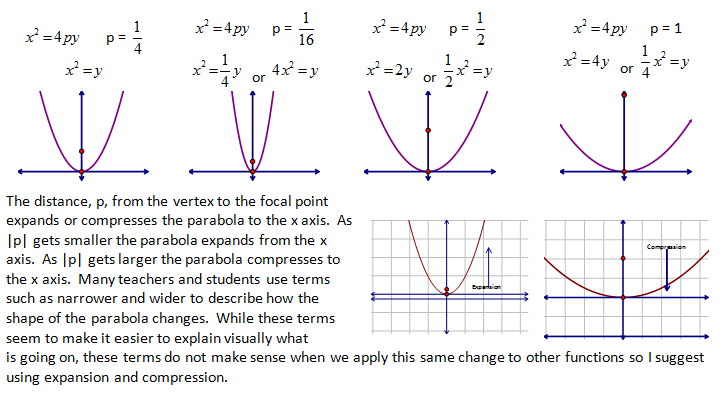
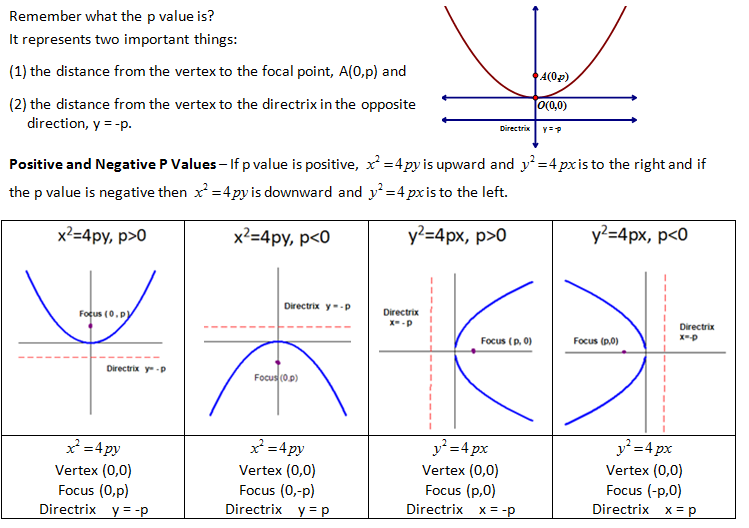
Understanding the forms of the equation and how the focal point, vertex and directrix relate to each other allows us to determine information from each other. The following examples display this connectivity.

The vertex and the p value allow us to determine anything we want to know about the parabola.
Working backwards is often more of a challenge for students, when given the equation and asked to determine the p value and the other key points of the parabola. You would think that this would be easier but it is not because the equation can be written in different forms and the solving often involves multiplying and dividing fractions (oh no…. not fractions!!!). The following examples display this process.


| Teacher Note: There are some position for the coefficient that are harder than others for students. Practice many different locations. |
|












