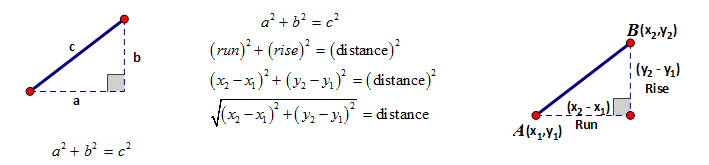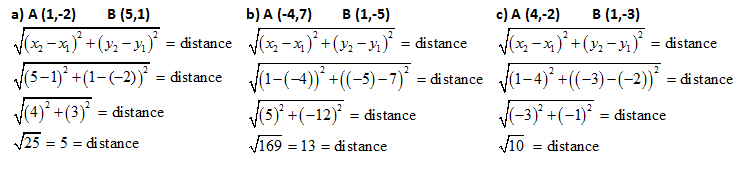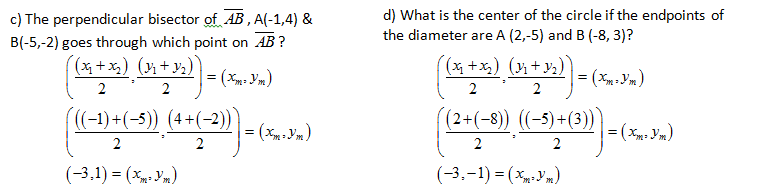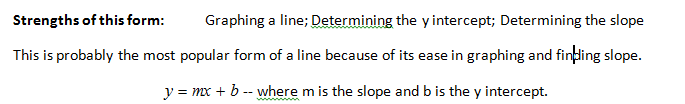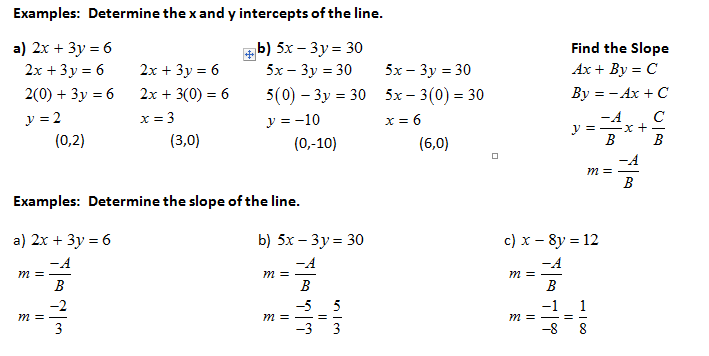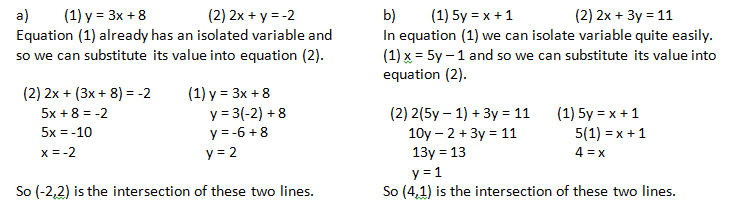CONCEPT 1 – Linear Equations
This objective asks us to analyze geometric relationships and figures using coordinates. To be able to do this we need to establish some foundational concepts – concepts that were introduced in Algebra I or earlier. Understanding functions and being able to use the slope formula, the distance formula, and the midpoint formula are some of those essential foundational concepts and skills. So while these may not be directly stated in the objective, it is an important that we review them before we proceed further. Because much of this is review I will approach it in brief.
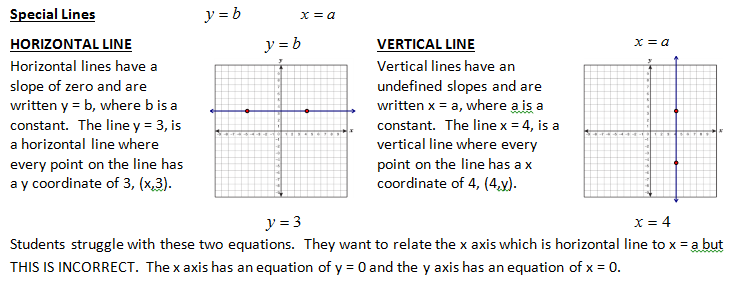
Linear equations are functions. What that means is that for each x value there is exactly one y value. The vertical line test is used to determine if something is a function or not because if the vertical line intersects the relation exactly once for all values of the domain, then it must be a function. All non-vertical linear equations are functions.

| Teacher Note: Horizontal and vertical line equations are ALWAYS TROUBLE!! Even through we have used these with dilations, directrix parabolas and a few other places... these still cause trouble. |
The Distance Formula – In an earlier objective we discussed how the distance formula is actually the Pythagorean Theorem. When not on the coordinate plane we refer to it as the Pythagorean Theorem and when we are on the coordinate grid, we refer to it as the distance formula but ultimately they are the same relationship. Once on the coordinate grid we are able to determine the length of the legs of the triangle by calculating the difference between x values and the difference between the y values.
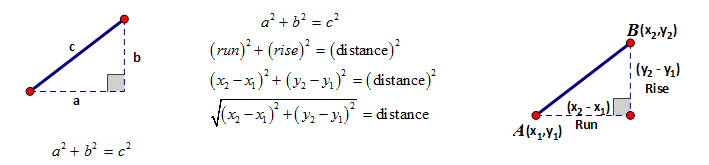
Using this formula we are able to easily calculate any distances found on the coordinate plane.
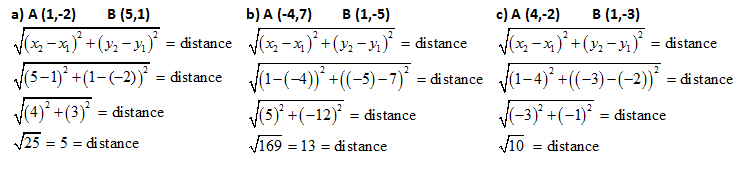
While the below examples don’t directly state the need of the distance formula, they would all be quite easily solved using it. It is a very powerful formula and it can be used for many different purposes.

Another way to test the question about whether the point is in the interior, the exterior or on the circle is to substitute the point into the equation. If the value comes out less than the radius, then it is in the interior, if it comes out equal to the radius, then it is on the circle, and if it comes out greater than the radius, then it is in the exterior.

Here are two examples where the midpoint formula could help us solve the problem.
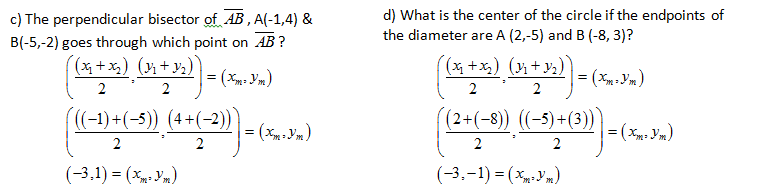
CONCEPT 2 – Equations of Lines
| Teacher Note: Before getting to the more advanced things we need to make sure that working with linear equation is comfortable. |
Writing, graphing and analyzing linear equations is also another essential foundational concept. Linear equations other than vertical and horizontal lines have multiple ways that they can be written. Each of the different forms has its own purpose - Its own strengths. The linear form that you will use will depend on what you are being asked to do or determine.
FORM -- Slope Intercept Form

FORM -- Point Slope Form
Strengths of this form: Easy to create an equation.

FORM -- Standard Form
Strengths of this form: Determining x and y intercepts; Determining the slope.
This form simplifies the process of solving for intercepts because by placing in zero values for x or y, the equation is ready to be solved for the y intercept or x intercept.
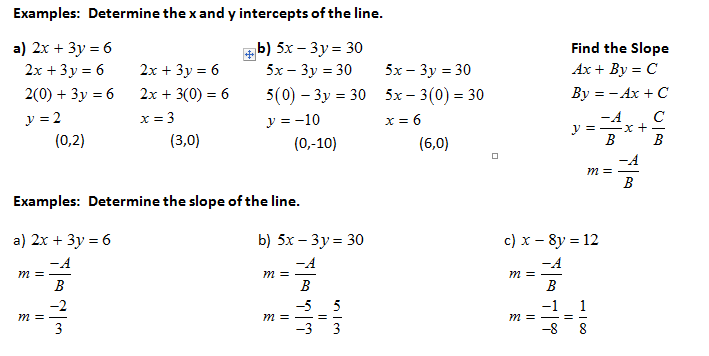
CONCEPT 3 – System of Linear Equations
A system of linear equations is a mathematical way of saying more than one line. In a system of linear equation we are usually trying to determine what points the equations have in common. A system of linear equations can have three different interactions – One solution, No solution and Infinite solutions.
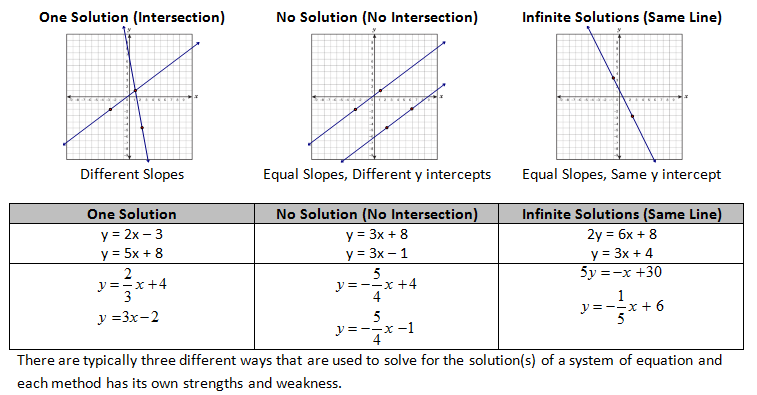
Technique 1 – Graphing
Strengths of this Technique: Quick and Visual Weakness: Inaccurate

Technique 2 – Substitution
Strengths of this Technique: Accurate Weakness: Difficult with coefficients other than 1
Because we are looking for the single point where both lines equal each other, the x and y values are the same value at that point for both lines. Each line has an infinite amount of points but together they only have one common point when they intersect. This allows us to use the x value of one line as the same x value in the other line and the same for y. One way to solve two equations with two unknowns is to substitute a variable value into the other equation. This is a method that we use when we can easily isolate the x or y variable.
Examples: Determine the intersection of the two lines
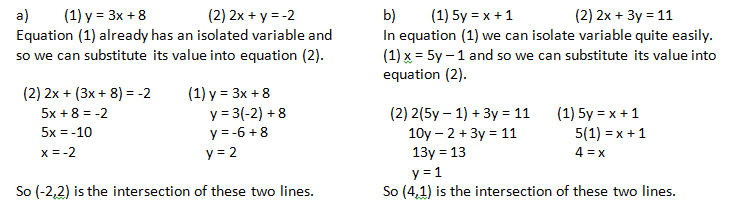
Technique 3 – Elimination
Strengths of this Technique: Accurate, Handles the type that substitution doesn’t do easily.
This technique works nicely when the variables don’t isolate very easily. The side benefit of learning this technique is that it prepares students for matrices and matrix operations. The idea of this method is to alter the equation or equations through multiplication so that one of the variables cancels either through addition or subtraction.
Examples: Determine the intersection of the two lines

CONCEPT 4 – System of General Equations
| Teacher Note: We increase the difficulty of systems by doing equations of other shapes and curves than just linear relationships. This is a nice way to mix geometry and algebra. |
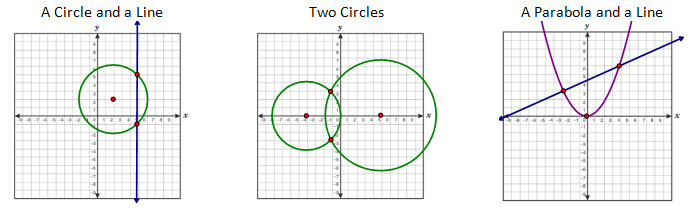
A system of equations does not always have to be with lines. A system of equations could be a line and a circle, a line and a parabola, two circles, etc… the list can go on and on. Ultimately, the process is the same as what we did with two lines.


Another technique that could be used to solve quadratic equations is factoring. Factoring only works in certain situations but can be much easier than the quadratic equation.

|