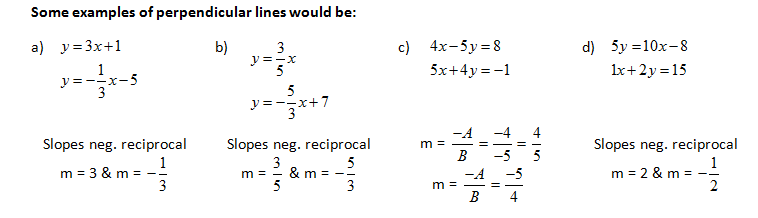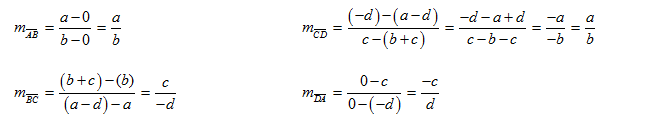CONCEPT 1 – Parallel Lines and Skew Lines
Parallel lines are two COPLANAR lines that never intersect. Most definitions that students (and some teachers) give leave out the word coplanar. Coplanar is an essential part of the definition because there are other types of lines that never intersect but are not parallel, these types of lines are called Skew Lines.
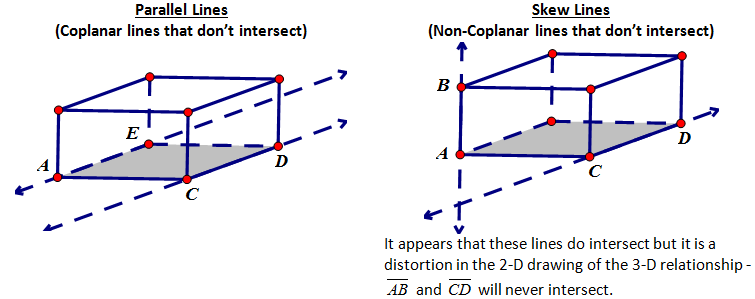
| Teacher Note: This distinction is often missed... we often accept the definition of parallel to be two lines that never intersect and this is NOT correct. |
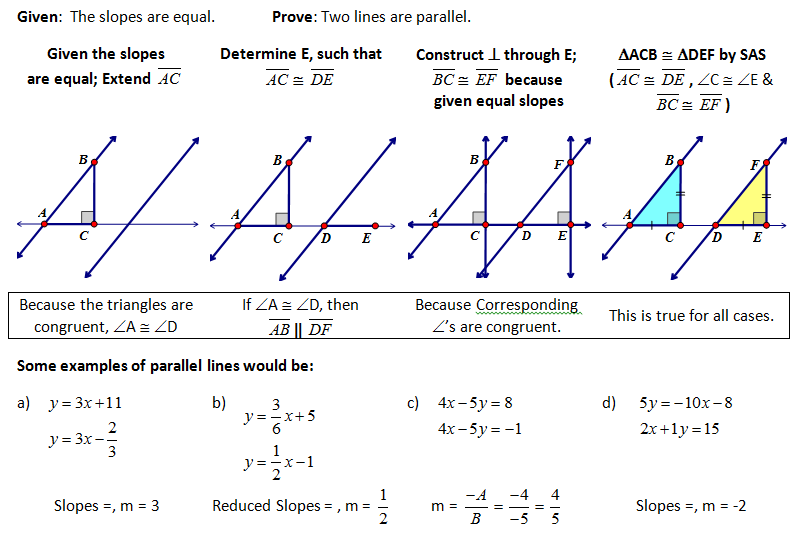
CONCEPT 2 – Parallel Lines and Slope
When we move from the general plane to the coordinate plane we notice that lines that never intersect have the same slope. This relationship can be proven without even using the coordinate plane which is very powerful because then we know that it works in all cases.
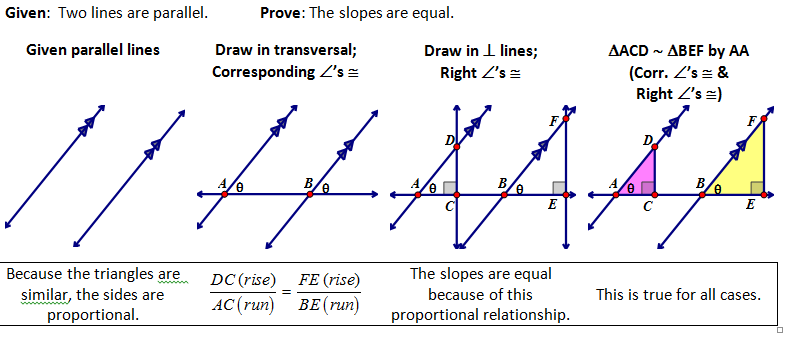
| Teacher Note: This is really nice!! Too often we just accept this relationship to be true... because it is obvious but this is a nice proof. |
It is important to establish the converse relationship as well, that if lines have the same slope, then they are parallel.
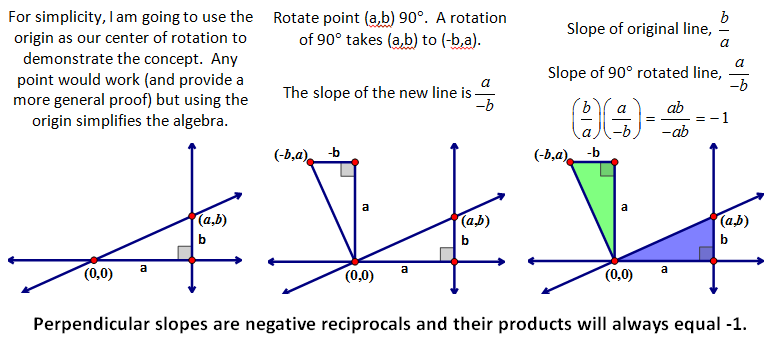
CONCEPT 3 – Perpendicular Lines and Slope
Perpendicular lines also have a slope relationship. Two perpendicular slopes have negative reciprocal slopes or in other words, the product of two perpendicular slopes is -1. I will prove this below.
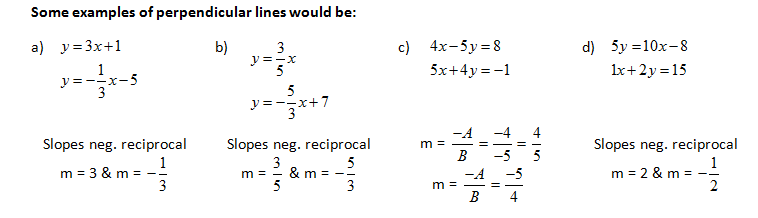
CONCEPT 4 – Equations of Parallel and Perpendicular Lines
Knowing the slope relationships of parallel and perpendicular lines helps us determine equations of these types of lines quite easily. Usually to generate the equation of a line we need a slope and a point, knowing that the relationship is either parallel or perpendicular ultimately provides us slope information.

Knowing these relationships help us describe many other situations. For example we can now determine the equation of a perpendicular bisector to a segment or a tangent line to a circle.

| Teacher Note: The reason I wanted to do this type of question in tihs objective instead of the last one is because many shapes that we classify have perpendicular and parallel relationships so it makes sense to handle it now. |
CONCEPT 5 – Using Slopes and Distances to Prove Relationships
Coordinates allow us to analyze all kinds of situations. Rene Descartes could not have foreseen the immense applications to the grid that allowed him to chart the path of the fly on his bed canopy. For example, if we are given four points in the plane we are able to determine the specific type of quadrilateral that it is and then from there apply its properties.
For example, prove that quadrilateral ABCD is a rectangle where A(2,-5), B(8,-3), C(7,0), and D(1,-2).
Coordinate proofs like this usually have more than one way to establish their proof. For instance in this case here are two possible ways (there are others as well). We could show that:


These kinds of proofs can be approached in many different ways… depending on the properties that you want to establish to verify the shape. Proofs of this type can also become more abstract by not listing physical coordinates of the vertices but instead variables. The process is the same but students struggle much more with type of problem because of the abstract nature of the variable coordinates.
For example, prove that quadrilateral ABCD is a parallelogram where A(0,0), B(a,b), C(a-d b+c), and D(-d,c). To do this I think the easiest method will be to establish that opposite sides are parallel so we will calculate the slope of all 4 sides and compare them.
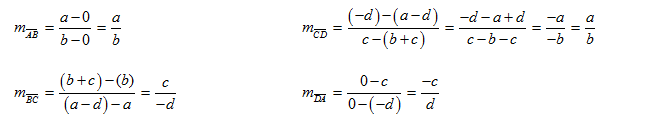
Opposite sides are parallelogram and so yes this is a parallelogram.
|