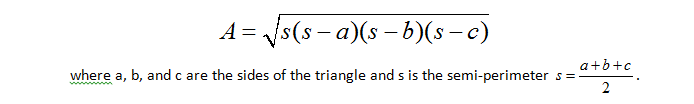CONCEPT 1 – Using Coordinates to find Perimeters
Perimeter is an easy thing to calculate using coordinates. Simply use the coordinates and the distance formula to determine the length of each side and then sum those values.

CONCEPT 2 – Using Coordinates to find Areas
There are a number of different ways to approach area on the coordinate grid and each approach depends on the situation that you are dealing with. We will start with some simple techniques and then progress to some that are a little bit more technical. You pick which technique is easiest for you to use. I really like the box technique; you will see its simplicity and its power.
One side is vertical or horizontal
Most area calculations involve a base and a height. Bases and heights must always be perpendicular to each other. So if one of the sides of the polygon is a horizontal or vertical line, then determining the base and the height can be quite easy. Length of horizontal and vertical segments can be counted out along the gridlines (the difference in the x or y values respectively). The height is also quite easy to determine because the height must be perpendicular to the base which means the height is also a horizontal or vertical segment.
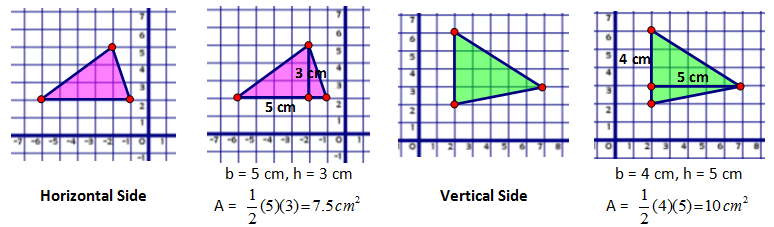
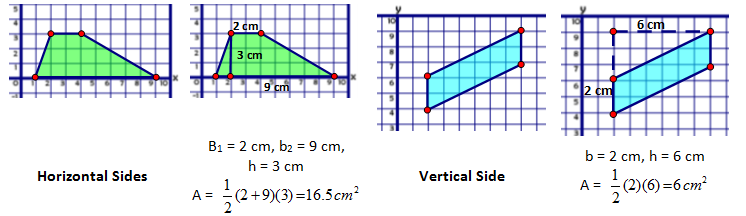
Many of the area problems we do have horizontal and vertical lines which make finding area quite simple but this technique is limited to only this type of problem.
| Teacher Note: The shearing technique that we learned in G.GMD.1 can definately be applied here as well. |
Box Technique
I really like this technique – it takes what could be a fairly difficult task to do and makes it very simple. For example, if you were asked to determine the area of DABC you can see that none of its sides are vertical or horizontal. Normally this would be difficult because it is hard to establish a base and a height.


The simplicity, speed and accuracy of this technique makes it my favorite.
| Teacher Note: Why do anything but the 'box' technique....? It is just so easy for even the most complex shapes. |
Finding the height using perpendicular lines
With certain polygons a height and a base is needed. The distance formula can easily ascertain the distance of one of the sides but the height is much more difficult when the base is not vertical or horizontal. In these cases we create the equation of the perpendicular line through the opposite vertex (the height) and then determine the intersection of these two lines to give us a way to determine the height of the polygon.
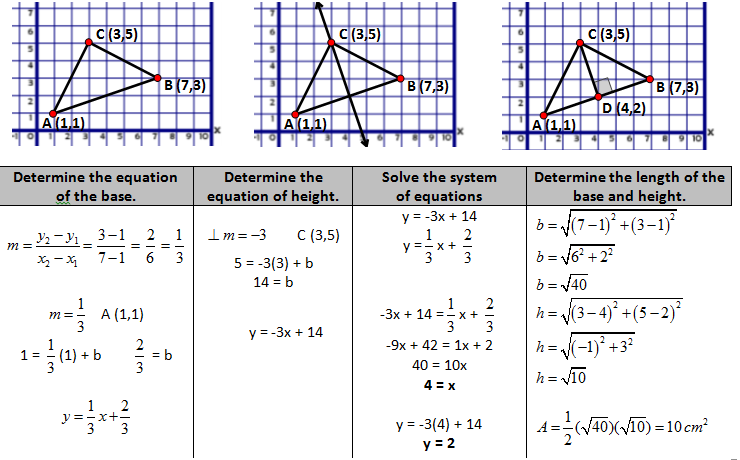
The truth is ….. why would you do this when you can do the box technique… this is for the algebra junkies!!!
| Teacher Note: I cover this just two apply the things that we had just done but it makes no sense to use these techniques for these situations. It is just a lot of work when there are much much simplier techniques. |
Heron’s Formula
Heron’s Formula is an interesting formula. It allows you to determine the area of a triangle using only the lengths of the sides of a triangle. What this means is that if you are given the three vertices of a triangle all you need to do is calculate the three distances and then plug their values into the formula to determine the area. This objective does not mention Heron’s Formula directly but I think it fits perfectly.
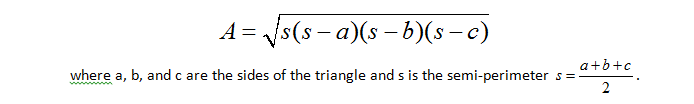


| Teacher Note: Heron's formula is great!! Don't feel the need to prove it but it has a great use because often we know the sides of the triangle but not its height. |


See... very simple to prove... :) |