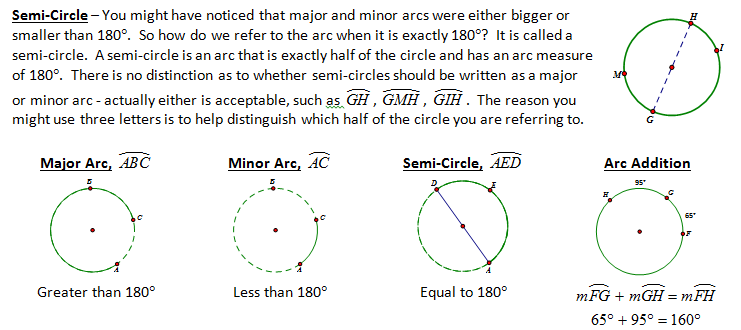
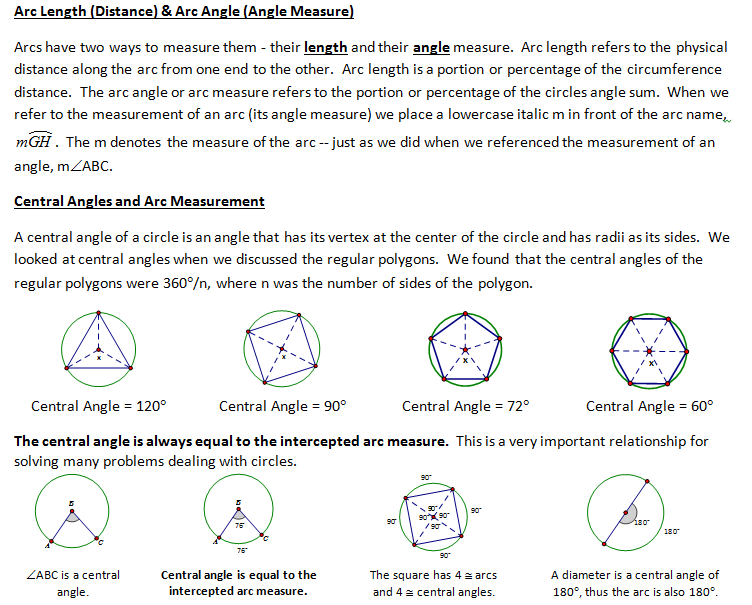
CONCEPT 1 – Circle Basics
Thus far we have done a number of things involving circles such as circumference, area, sectors, constructions, and regular polygons and yet we haven’t looked specifically at the properties and relationships found in a circle. The first step in this process is to define the circle.
A circle is the locus of all points that are equidistant from a given point,
called the center. The distance from the center to its points is called the radius.
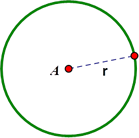 The word locus can be translated to mean ‘the set of’. Thus a circle is the set of all points that are equidistant from a given point. When we name a circle we refer to it by its center, so for example the circle to the right is called Circle A. The word locus can be translated to mean ‘the set of’. Thus a circle is the set of all points that are equidistant from a given point. When we name a circle we refer to it by its center, so for example the circle to the right is called Circle A.
The radius of the circle is the fixed distance from the center to the edge of the circle, so for example the circle to the right has a radius of r.
A circle is quite unique because only a single value defines it shape even through it’s a two dimensional object. Since all aspects of a circle’s size depends on the length of its radius, we can change the size of any circle by simply dilating the radius by a scale factor to either make it bigger or smaller.
Circumference – We have already looked at this in an earlier objective but the circumference of a circle is the distance around the circle and is calculated by C = Πd or C = 2Πr.

CONCEPT 2 – Tangent Properties
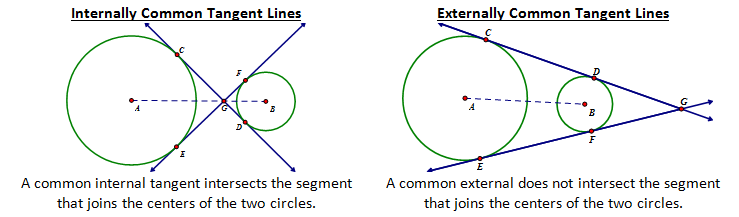
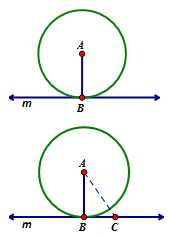
As defined previously, a tangent line intersects the circle exactly once at a point called the point of tangency. In the diagram to right, line m is a tangent line and point B is the point of tangency. Tangent lines can possibly intersect more than one circle at a time. For example you can have internally common tangents or externally common tangents.
|
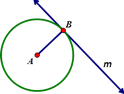 |
Theorem – If a line is tangent to a given circle, then the tangent line is perpendicular to the radius at the point of tangency. |
 |
Proof of the Theorem -- The proof of this theorem uses an indirect approach. An indirect proof works as follows – To prove something is true you assume that the opposite is true and by creating a contradiction (or impossible situation) to that assumption you actually prove that the opposite then must be true. It is kind of a sneaky approach but in many cases it is easier to prove what something isn’t than it is to prove what it is. Many high level proofs use an indirect approach.
So our given is tangent line m. This means that the line m intersects the circle at point B, a point of tangency, and ALL other points on line m are exterior to the circle. We are going to assume (the opposite of what we believe) that the angle formed at point B is NOT a right angle (NOT 90°) and thus there exists another segment that would be the perpendicular and represent the shortest distance from the tangent line to point A. This creates a contradiction because for any point C it will be in the exterior of the circle and thus a greater distance than the radius length AB. It is impossible for AC to be shorter than AB because point C is in the exterior of the circle and B is on the circle. This contradiction establishes that the opposite of our assumption is true - that the point of tangency forms a right angle with the tangent line.
|
 |
Ultimately, when you are told that a line is tangent to a circle you gain a right angle between the tangent line and the radius with endpoint at the point of tangency. Right angles lead to right triangles… and right triangles lead to questions about special right triangles, trigonometry, and the Pythagorean Theorem (to name a few).


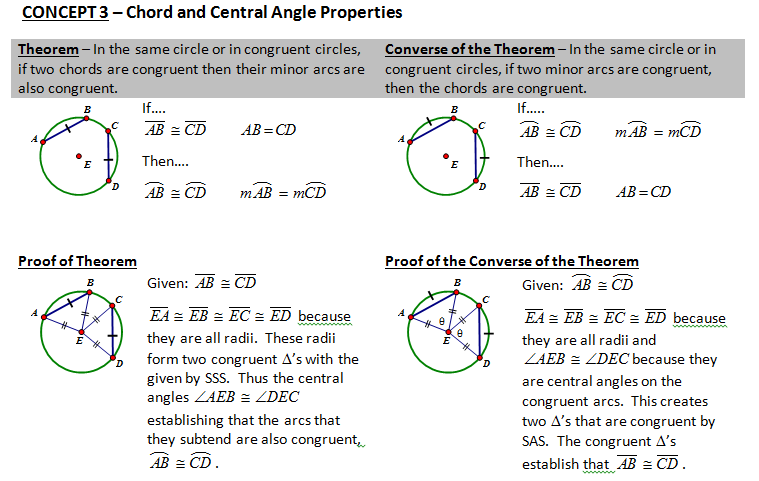
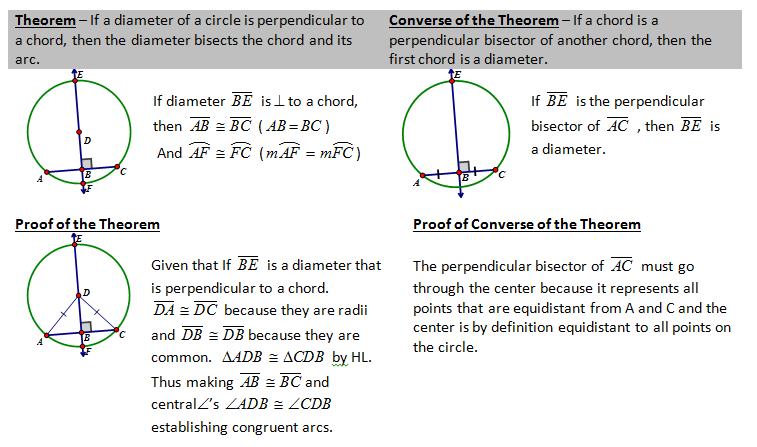
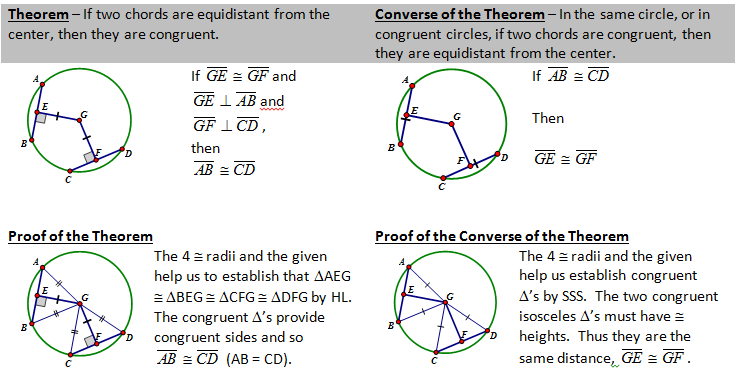
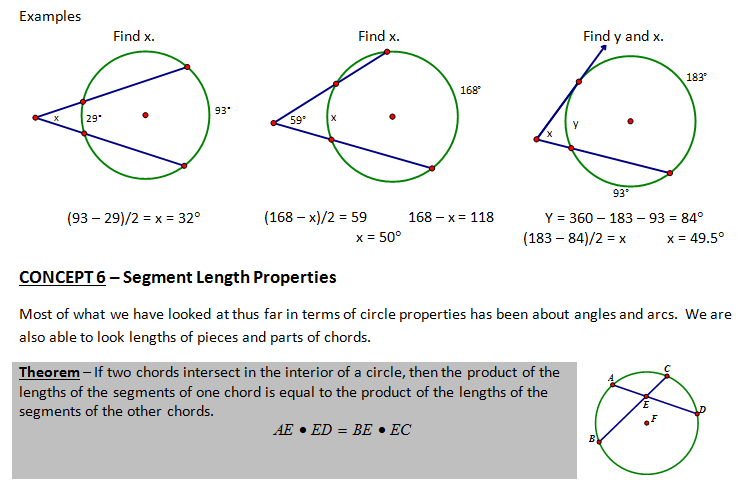
CONCEPT 4 – Inscribed Angles Properties
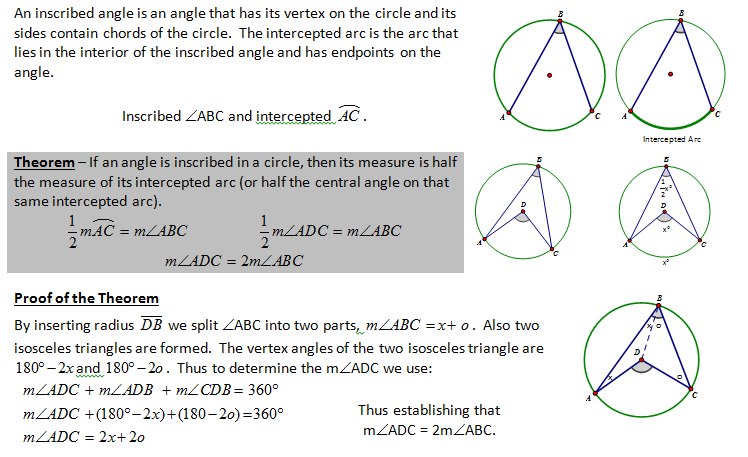

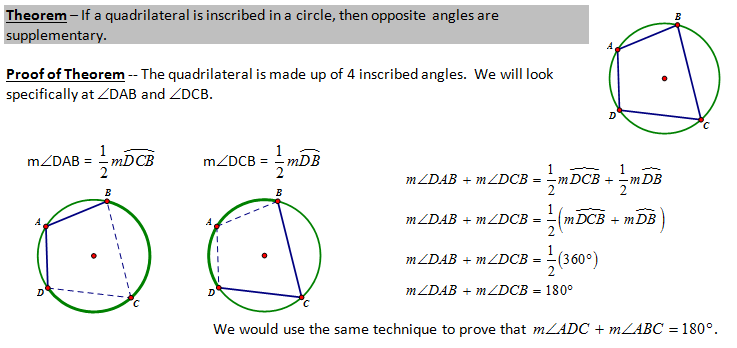
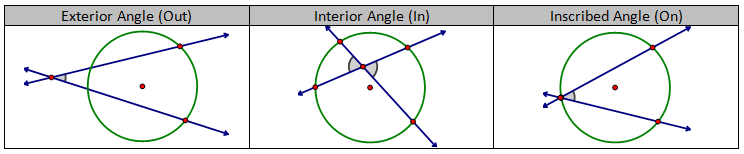
CONCEPT 5 – Internal, External and Tangental Angle Properties
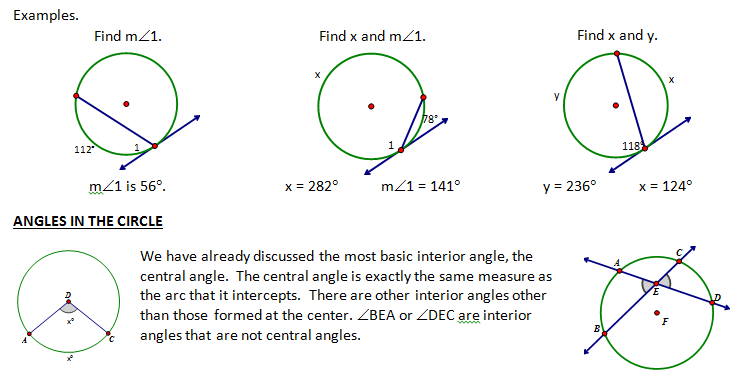
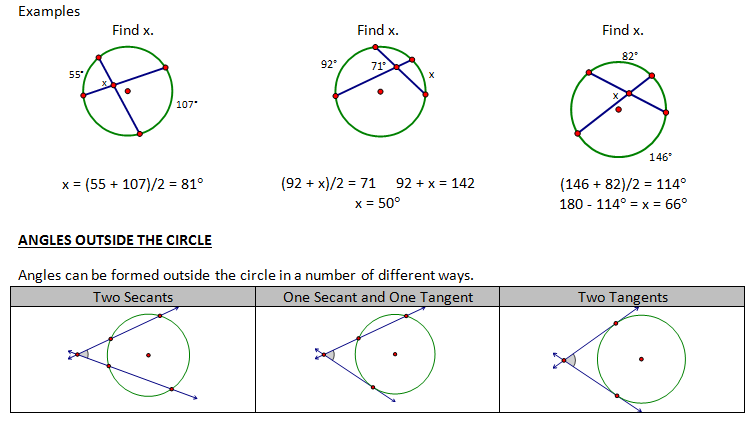
Inscribed and central angles are NOT the only types of angles that are formed when dealing with circles. Lines can intersect to form angles in the exterior, interior and on the circle.

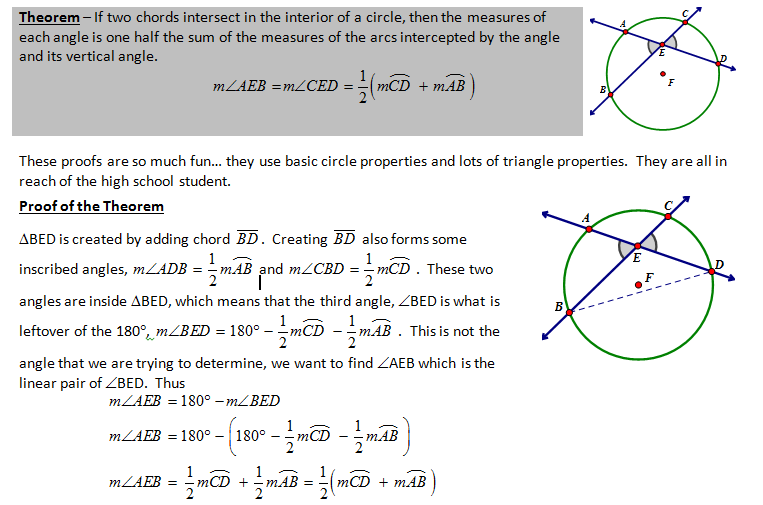
| Teacher Note -- The above proof could be simplified a bit if you use the exterior angle theorem. |
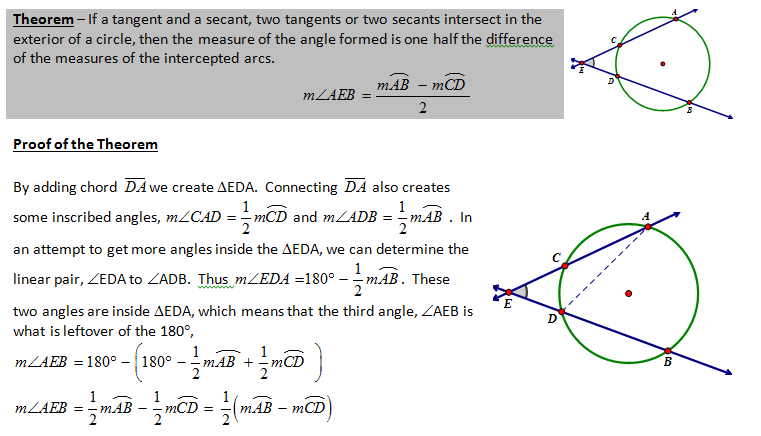
| Teacher Note -- The above proof could be simplified a bit if you use the exterior angle theorem. |
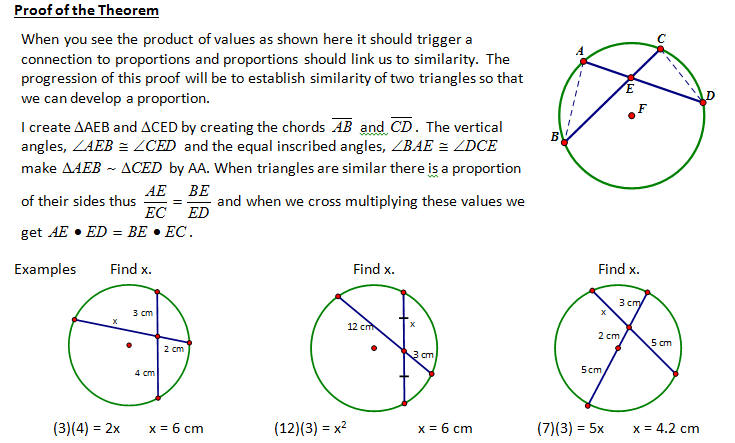
| Teacher Note -- The above below is a wonderful review of similarity and similarity proofs from Unit #2. |
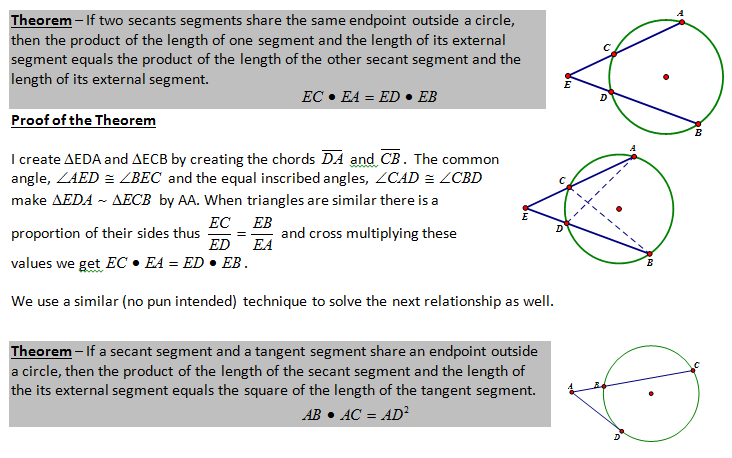
| Teacher Note -- The above below is a wonderful review of similarity and similarity proofs from Unit #2. |
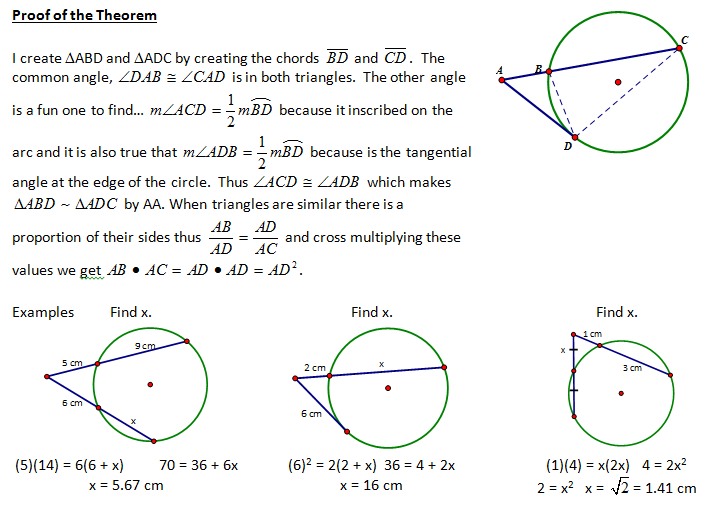
|


 The word locus can be translated to mean ‘the set of’. Thus a circle is the set of all points that are equidistant from a given point. When we name a circle we refer to it by its center, so for example the circle to the right is called Circle A.
The word locus can be translated to mean ‘the set of’. Thus a circle is the set of all points that are equidistant from a given point. When we name a circle we refer to it by its center, so for example the circle to the right is called Circle A. 






















