- HOME
- Organize
- UNIT #1
- G.CO - Overview
- G.CO.1 - Definitions
- G.CO.2 - Functions & Isometries
- G.CO.3 - Symmetries of Shapes
- G.CO.4 - Transformations
- G.CO.5 - Transformation Sequences
- G.CO.6 - Concepts of Congruence
- G.CO.7 - Congruence
- G.CO.8 - Congruence Criteria
- G.CO.9 - Proof (Lines/Angles)
- G.CO.10 - Proof (Triangles)
- G.CO.11 - Proof (Quadrilaterals)
- G.CO.12 - Basic Constructions
- G.CO.13 - Advanced Constructions
- UNIT #2
- G.SRT - Overview
- G.SRT.1 - Dilations
- G.SRT.2 - Similarity
- G.SRT.3 - Similarity Criteria
- G.SRT.4 - Proof (Triangles)
- G.SRT.5 - Geometric Mean & SRT
- G.SRT.6 - Trigonometric Ratios
- G.SRT.7 - Sine & Cosine Relationship
- G.SRT.8 - Solve Problems
- G.SRT.9 - Area Formula
- G.SRT.10 - Derive Sine/Cosine Laws
- G.SRT.11 - Apply Sine/Cosine Laws
- UNIT #3
- UNIT #4
- UNIT #5
- UNIT #6
- G.CP - Overivew
- G.CP.1 - Sample Spaces
- G.CP.2 - Independence
- G.CP.3 - Conditional Probability
- G.CP.4 - Two Way Frequency Tables
- G.CP.5 - Probability Everyday
- G.CP.6 - Given That Rule
- G.CP.7 - Addition Rule
- G.CP.8 - Multiplication Rule
- G.CP.9 - Permutations/Combinations
- G.MD.6 - Fair Decisions
- G.MD.7 - Analyze Decisions
- Resources
- Interaction



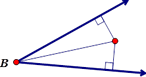 gles into two congruent angles but in this construction that is secondary to the fact that the angle bisector represents all points that are equidistant to the two sides of the angle. This can be proven using congruent triangles and the AAS congruency theorem (bisected angle, right angle, and common side). The congruent triangles tell us that all points are equidistant to the sides of the angle.
gles into two congruent angles but in this construction that is secondary to the fact that the angle bisector represents all points that are equidistant to the two sides of the angle. This can be proven using congruent triangles and the AAS congruency theorem (bisected angle, right angle, and common side). The congruent triangles tell us that all points are equidistant to the sides of the angle.