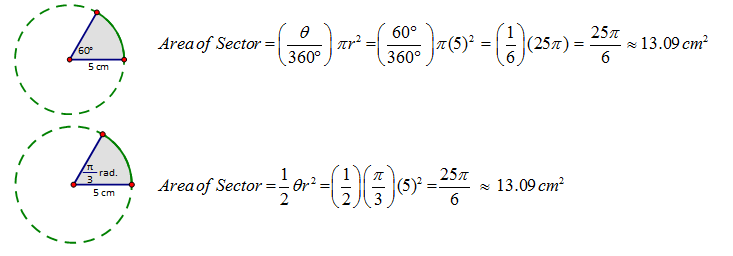CONCEPT 1 – What is a radian?
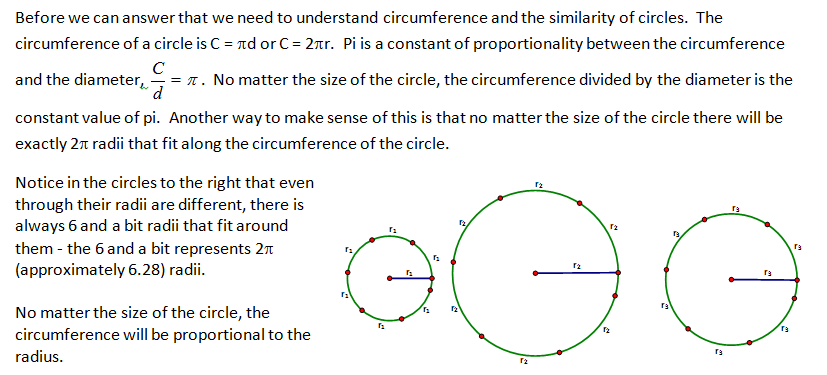
Up to this point we have measured angles only in terms of degrees. In most work involving applications of trigonometry, angles are measured in degrees. In more advanced work in mathematics, the use of radian measure of angles is preferred. Radian measure allows us to treat trigonometric functions and other angle-based functions as functions with domains of real numbers (distances), rather than angles.
So what is a radian?
| Teacher Notes -- One of the reasons that we identified that circles are all similar it to build the concepts for radians. We need to know that circles are all similar and thus proportional to each other helps us understand why 1 radian is the same for all circles. |
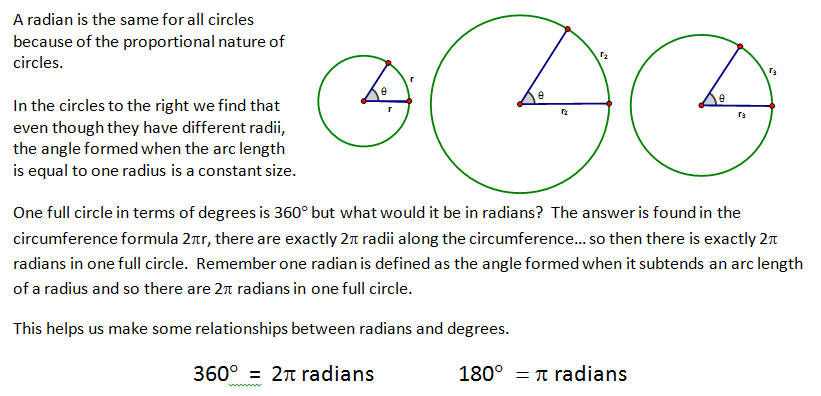
A radian is the central angle that subtends an arc length of one radius.
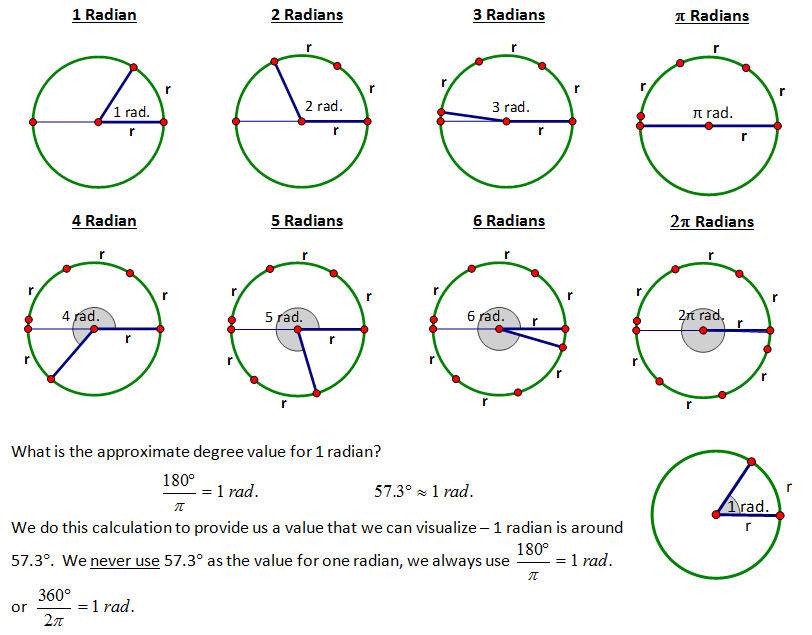
| Teacher Notes -- We are so use to degrees that if I say 240° we know exactly where that is but if I say Π/3 radians it is so hard for students to visualize it... I like to spend time just discussing what size do we expect from certain radian measures. So much of radian understanding comes from understanding fractions. |
CONCEPT 2 – Converting between Degrees and Radians
One of the necessary skills is to be able to convert between degrees and radians. These two types of angle measures have different strengths and weaknesses in certain areas and so converting in and out of them is an important skill. We will see how some of the typical degree based formulas become greatly simplified when working in radians.
To be able to convert between two different measurements we need two values where they have the same value – one complete circular revolution. In that case the degree measure is 360° and the radian measure is 2Π radians. So 360° = 2Π radians.


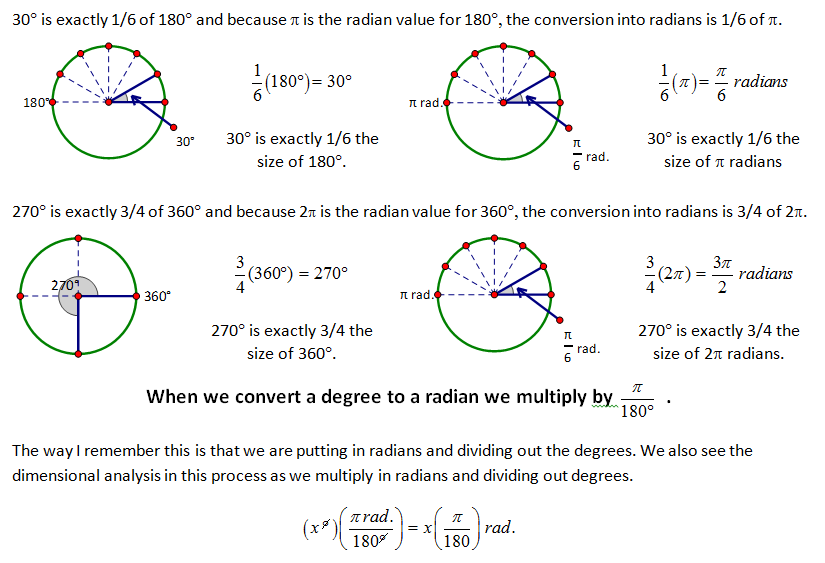

| Teacher Notes -- So many teachers just teach students to convert to degrees and then work in degrees..... this is so far from this objective. Arc length and area become very simple calculations when the angle measure is in radians... work in RADIANS!!! |
CONCEPT 3 – Radians and Arc Length



CONCEPT 4 – Radians and Area
Much like the way we dealt with the length of an arc we do the same with the area of a sector. Think of a sector as a part or percentage of the whole area of the circle. We adjust the area formula slightly by creating a percentage of the whole, in the case of degrees it is a percentage of 360° and in the case of radians it is a percentage of 2Π.

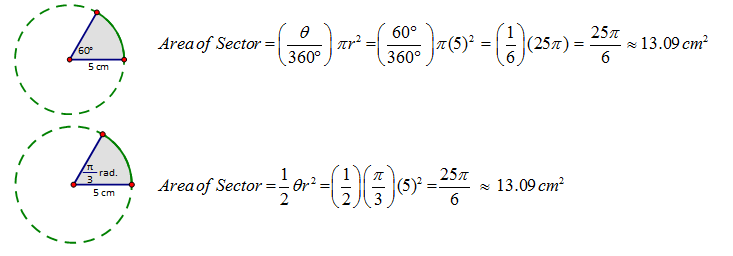
CONCEPT 4 – Application Problems
Pulleys & Gears

|