CONCEPT 1 – Independence
When working with probabilities we often perform more than one event in a sequence this is called a compound probability. Compound probabilities are more complex than a single event probability to compute because the first event might affect the probability of the second event happening.
 For example, the probability of getting a head on a single flip of a coin is ½. If you flip the coin and get a head, the second flip’s probability of getting a head is still ½ because the results of the first flip does not in any way affect the second flip. The second flip has the exact same probability as if it was the first flip, ½. When the first action does not affect the second action’s probability in any way the events are known to be INDEP For example, the probability of getting a head on a single flip of a coin is ½. If you flip the coin and get a head, the second flip’s probability of getting a head is still ½ because the results of the first flip does not in any way affect the second flip. The second flip has the exact same probability as if it was the first flip, ½. When the first action does not affect the second action’s probability in any way the events are known to be INDEP ENDENT. ENDENT.
In contrast, if you have a jar of cookies with 7 chocolate chip cookies and 3 peanut butter cookies the probability of getting a chocolate chip is 7/10 and the probability of getting a peanut butter cookie is 3/10. Is the probability of getting a peanut butter cookie still 3/10, if you first pick out a chocolate chip cookie and eat it? Of course not, the probability of getting a peanut butter cookie now is 3/9 because a chocolate chip cookie is gone from the jar. The second selection is affected by the first selection, thus these two events are NOT INDEPENDENT.
Definition: Two events, A and B, are independent if the fact that A occurs does not affect the probability of B occurring (or vice versa).
Some other examples of independent events are:
-- Getting a head after tossing a coin AND selecting a purple marble from a bag.
-- Getting on head after tossing a coin AND rolling a 2 on a single 20-sided die.
-- Choosing a jack from a deck of cards, replacing it, AND then choosing a king as the second card.
What is the probability of rolling a 6 AND then getting a head on a coin flip?
These two events are independent - the die could roll any number of times and it would in no way influence the flip of the coin. Let us use a set list, a tree and a Venn diagram to understand this problem.
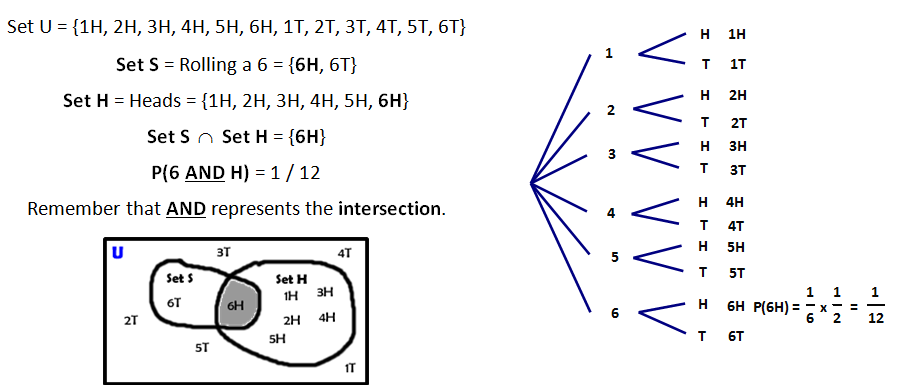
To find the probability of two independent events that occur in sequence, find the probability of each event occurring separately, and then multiply the probabilities. This multiplication rule is defined symbolically below. Note that multiplication is represented by AND.


Understanding independence is critical to probability because we must always take into account how one event affects the next event.
| Mutually exclusive and independence are always being confused. Take time to distinquish these two concepts because they are very different. |
CONCEPT 2 – Mutually Exclusive and Independence
A common misunderstanding is that independence is the same thing as being mutually exclusive. I get why this is confusing, to be independent in a typical English language context means to be alone or separate which is basically what we understand mutually exclusive to mean. This definition of independence is NOT the mathematical one. Independence is about whether one event affects another event’s probability or not.
Mutually exclusive sets are those that don’t share any elements and independent sets are those that don’t impact each other’s probabilities.
Mutually exclusive is about the sharing of elements,
and independence, is about affecting each other.
|
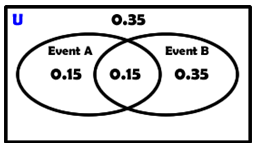
In the example to the right, event A and event B are NOT MUTUALLY EXCLUSIVE because there is an intersection between the two sets.
But Events A and Event B are INDEPENDENT because
P(A) · P(B) = (0.3)(0.5) = 0.15 P(A AND B) = 0.15
So here is one example where mutually exclusive and independence obviously are two different things!! |
 |
CONCEPT 3 – Replacement and No Replacement
The terms replacement and no replacement get used a lot in compound probabilities problems because they describe what you did with the first thing that you selected… did you put it back or did you keep it?
P (Getting a green marble, replacing it, and getting a green marble) Independent
P (Picking a black queen, not replacing it, and getting an ace) Not Independent
These two words are HUGE clues as to whether the events are going to be independent or not.
REPLACEMENT
|
Because the item is replaced, it resets the event back to the original arrangement and no probabilities are altered. Thus REPLACEMENT tells us that the events are INDEPENDENT.
|
| NO REPLACEMENT |
Because the item is NOT replaced, the probabilities are altered. Thus NO REPLACEMENT tells us that the events are NOT INDEPENDENT. |
| Independence is a major topic for this unit. Understanding how to test for independence is very important. Relate this to a Venn diagram. |
CONCEPT 4 – Testing for Independence
We can use the formal relationship of P (A and B) = P(A) · P(B) to test independence. Here are three examples of how we could use probabilities to determine if they are independent of each other.
Example #1 P(A) = 0.8 P(B) = 0.4 P(A and B) = 0.2
These are Not Independent because P(A) · P(B) = (0.8)(0.4) = 0.32 and this is not
the same as P(A and B) = 0.2 provided.
Example #2 P(A) = 0.6 P(B) = 0.5 P(A and B) = 0.3
These are Independent because P(A) · P(B) = (0.6)(0.5) = 0.30 and this is
the same as P(A and B) = 0.3 provided.
The same kind of test can occur but the information can be given in Venn diagram form.
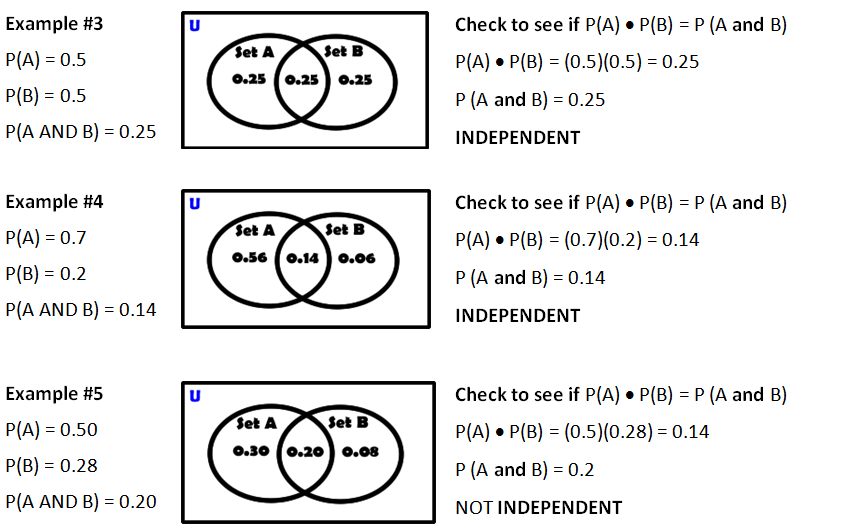
|


 For example, the probability of getting a head on a single flip of a coin is ½. If you flip the coin and get a head, the second flip’s probability of getting a head is still ½ because the results of the first flip does not in any way affect the second flip. The second flip has the exact same probability as if it was the first flip, ½. When the first action does not affect the second action’s probability in any way the events are known to be INDEP
For example, the probability of getting a head on a single flip of a coin is ½. If you flip the coin and get a head, the second flip’s probability of getting a head is still ½ because the results of the first flip does not in any way affect the second flip. The second flip has the exact same probability as if it was the first flip, ½. When the first action does not affect the second action’s probability in any way the events are known to be INDEP ENDENT.
ENDENT.



