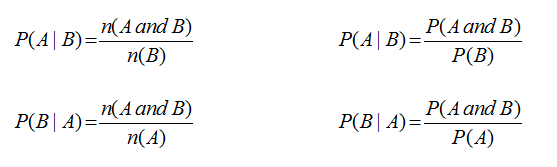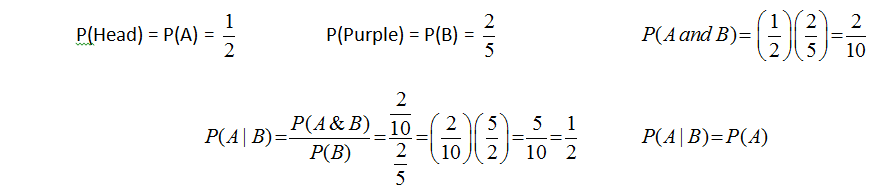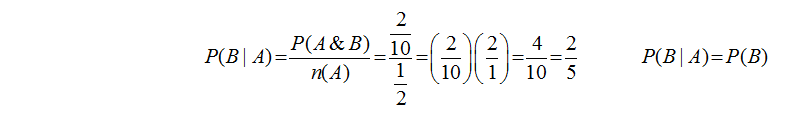CONCEPT 1 – Conditional Probability
A compound probability is when two or more events happen in a sequence. Compound probabilities are much more complex to calculate than single event probabilities because it is possible for the first event to alter the probability of the second event. When one probability is determined after an earlier event has already occurred it is called a conditional probability. A conditional probability is notated as:
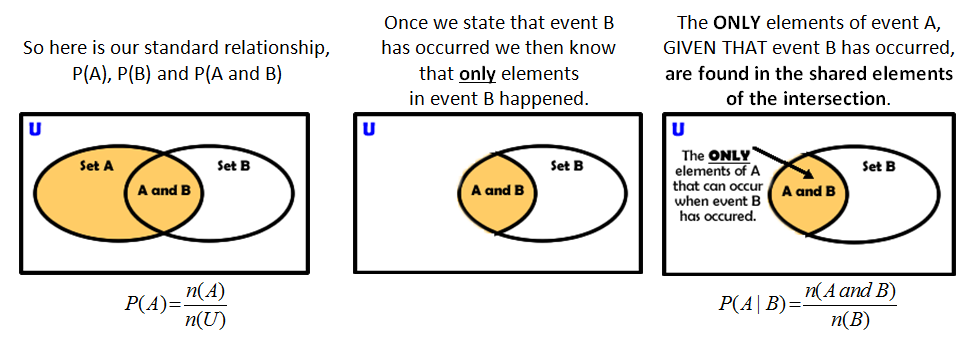
| Using the Venn diagram is great help to visualize and understand conditional probability. The GIVEN THAT statement gains meaning as you see the Venn diagram only display the probability of the given event A. It also nicely shows that the only elements for A are found in the intersection. |
P(A|B) - which states the probability of event A GIVEN THAT event B has occurred.
A visual way to make sense of this idea is found nicely in a Venn diagram.
This would also be true when looking at the P(B|A) as well.
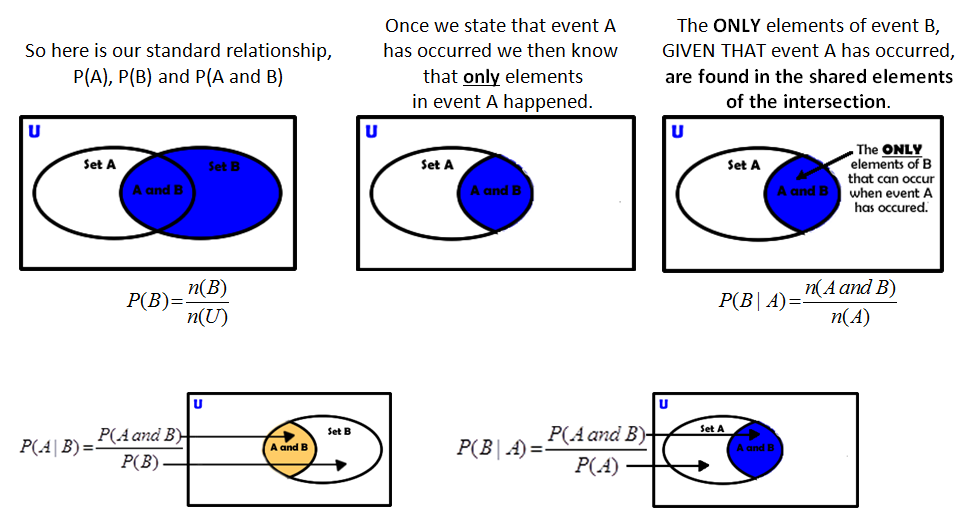
The formulas for calculating the conditional statements are provided below.
CONCEPT 2 – Conditional Probability and Independence
Earlier we found out that if two events are independent of each other, then P(A and B) = P(A) • P(B). Notice that because the two events were independent the second event’s probability was not impacted by the first event in anyway. Thus when dealing with two independent events the conditional probabilities are also not affected by the other event occurring previously. Thus
P(A|B) = P(A) P(B|A) = P(B)
because the fact that one occurred first makes NO IMPACT on the probability of the second one occurring.
Example #1 - Flipping a coin and then picking a marble from a bag are two independent events. So if a bag of marbles contains 2 Purple, 1 Green and 2 Orange, what is the probability of getting a purple, if you knew that a head was flipped first, P(Purple|Head)?
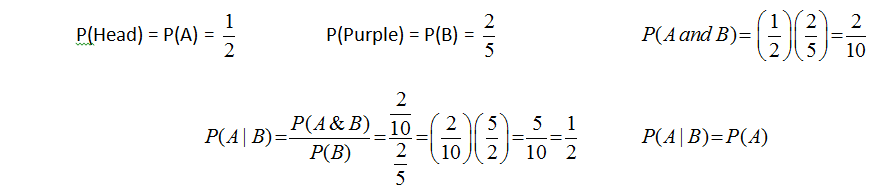
Notice that P(A|B) = P(A) when event A and event B are independent. |
If events A and B are independent then it should also be true that P(B|A) = P(B). Let’s test that conditional probability as well.
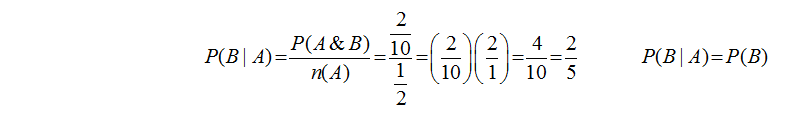
Notice that P(A|B) = P(A) when event A and event B are independent. |
If the two events are independent of each other, then P(A|B) = P(A) and P(B|A) = P(B). Event B has no effect on event A’s probability and event A has no effect on event B’s probability. In other words, event B could happen as many times as it wants and it will never alter the original probability of event A or event A could happen as many times as it wants and it will never alter the probability of event B.
If event A is independent of event B,
then it would also of course be true
that event B is independent of event A. |
We can use this new relationship, that if two events are independent then P(A|B) = P(A), to help us determine if two events are independent or not.
From the diagram we can determine that: P(A) = 0.25
If event A and B are independent then having event B occur first should not change the probability of event A in any way.
When event B happens only the elements within that set can occur.
This limits our chances of event A occurring to ONLY the elements of A that are shared with elements of B - the intersection of A and B. If the P(A|B) = P(A), then event A and event B are independent of each other and if P(A|B) ¹ P(A) then they are not independent. |
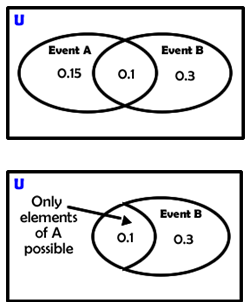 |

Notice that event B happening did not alter the probability of A happening.
THUS THEY ARE INDEPENDENT OF EACH OTHER. |
| These two tests for independence are HUGE ideas for this unit. Make sure that they understand both of these tests. This will help us later when we do conditional proabilties of dependent events. |
CONCEPT 3 – Tests for Independence
Now there are TWO tests for independence.

|