CONCEPT 1 – Conditional Probability and Dependence

When determining compound probabilities we found the relationship for independent events to be a very simple multiplication rule, P(A and B) = P(A) • P(B).  The occurrences of two independent events in a sequence don’t alter the probabilities of each other occurring, thus we can multiply their values together.  When the two events are NOT independent then of course they affect each other and their probabilities are altered or changed by one another.  The calculation of a probability that follows a previous event is called a conditional probability.  The phrase GIVEN THAT denotes a conditional situation in which something has already occurred first.  The notation for this relationship is:

P(A|B) this reads the probability of Event A, GIVEN THAT Event B has occurred.

In the first example, we have two independent events.  The flipping of a coin will not in any way affect the selection of the marble.  Because they are independent we learned in an earlier objective that:

P(A|B) = P(A)               P(B|A) = P(B)

In the second and third example, knowing that the roll was even or that the roll was doubles will definitely affect the probability of the second event and so when events are dependent conditional probability will not match the original probability.

P(A|B) ¹ P(A)              P(B|A) ¹ P(B)

In the example below we select a marble, keep it and then select again.  This of course will create an dependent situation because of keeping the selected marble out of the bag.

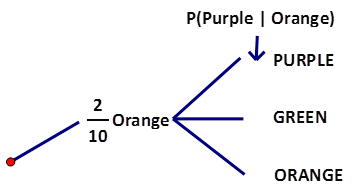
A bag of marbles has 2 orange, 5 purple and 3 green marbles.  Two marbles are chosen, without replacement.  Part of the tree diagram to this problem is displayed to the right.  To calculate the probability of getting a purple given that an orange had been selected first and not returned is a conditional probability. One less marble but all 5 purple still in the bag creates, P(Purple|Orange) = 5/9.   In this same relationship the P(Orange|Orange) = 1/9 because there is one less marble and one less orange GIVEN THAT orange had already been selected.

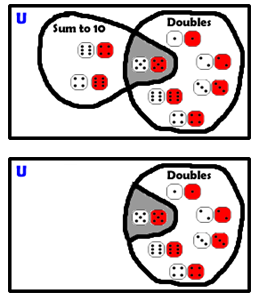
A way to make sense of this new relationship is to go back to our Venn diagrams.  Let us look at the example of rolling two dice and summing their values.  The sample space for this compound probability is (6)(6) = 36.

Set A = Sum of 10  = {(4,6), (6,4), (5,5)}                                P(A) = 3/36   Set B = Doubles  = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}      P(B) = 6/36   Set A  Set B = {(5,5)}                       P (A and B) = 1/36
What is the probability of getting a sum of 10 with 2 dice, GIVEN THAT doubles were rolled?   P(A|B) = 1/6 The condition is that doubles occurred first.  This reduces the number of possible outcomes and the intersection is the only values of event A possible.

Notice that P(A|B) = 1/6 but P(A) = 3/36

P(A|B) ¹ P(A) and so they events are not independent!!

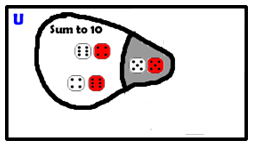
What is the probability of getting doubles, GIVEN THAT a sum of 10 was rolled?   P(B|A) = 1/3 The condition is that sum of 10 occurred first.  This reduces the number of possible outcomes and the intersection is the only values of event B possible.

Notice that P(B|A) = 1/3 but P(B) = 6/36

P(B|A) ≠ P(B) and so they events are not independent!!

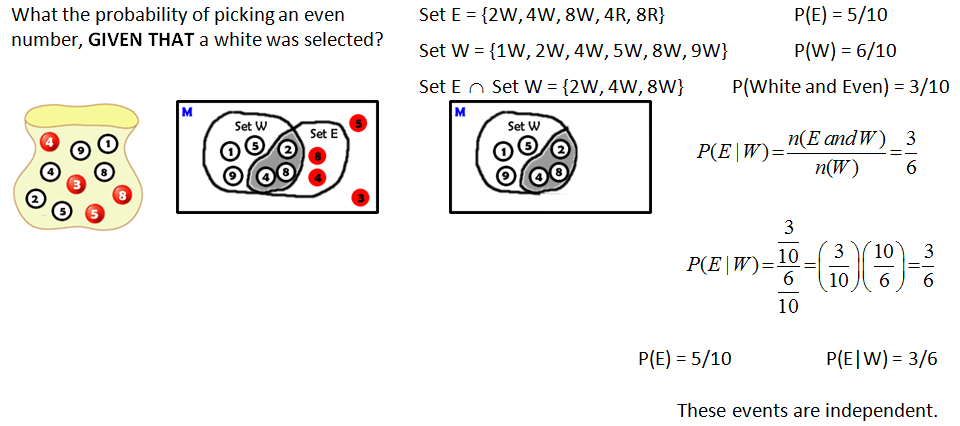
Let us look at another example, what is the probability of rolling a number greater than 4 on a single roll of a die, given that you know the number was even? 

CONCEPT 2 – Conditional Probability and Mutually Exclusive
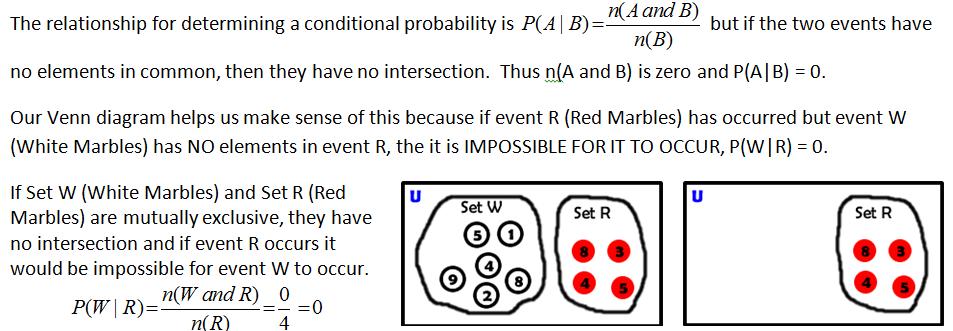