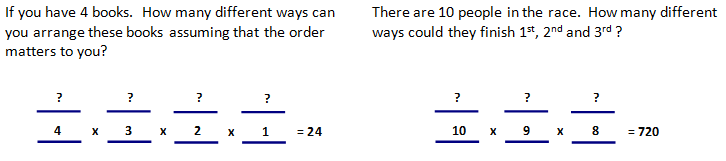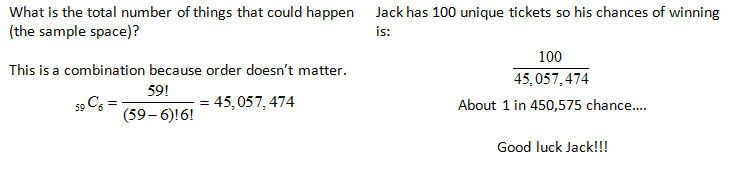CONCEPT 1 – Counting Principles
In calculating probabilities we often need to determine either the total number of possible outcomes or the total number of successful outcomes. In many cases the outcomes are easy things to count… red aces, blue marbles, coin flips, etc.. but sometimes determining these values can be a little more complex.
For example, Jimmy remembers the first 3 digits of Randy’s phone number but not the last 4. How many different possible numbers are there? 248 - ____ ____ ____ ____
There are 10 different digits 0 – 9 for each spot so there would be 10 • 10 • 10 • 10 = 10,000 different phone numbers. So Jimmy has a 1/10,000 chance of getting the number correct….. Good Luck Jimmy!!!
As mentioned in an earlier objective, the fundamental counting principle is a powerful tool to helping us with problems like this.
| FUNDAMENTAL COUNTING PRINCIPLE |
| If you can choose one item from a group of M items and a second item from a group of N items, then the total number of two items choices is M • N. |
The FCP allows for the use of the same item to be used more than once. For example, in the telephone example above 248 – 1212 is a perfectly fine result. It is for this reason that we multiply 10 • 10 • 10 • 10 because the numbers 0 – 9 can be used for all four spots if necessary.
This is not always the case, sometimes when we use a number or an item it cannot be used again, for example, if there are four people and we want to know how many different ways that they could finish a race, a person cannot come in 1st and in 4th. Thus 4 • 4 • 4 • 4 doesn’t make sense – once a person places they cannot be used again.
CONCEPT 2 – Permutation (Order Matters)
Let’s try a little different problem. Four bands are going to perform at the Friday Night Jam Session. How many different ways could the schedule for the night be arranged?
The way I make sense of this is 4 different bands could go first, since one has been picked 3 different bands could go in the next place, then 2 and then finally 1…. 4 • 3 • 2 • 1 = 24 different ways. In mathematics when we multiply n (n – 1) (n – 2) …. We call that a FACTORINAL AND IT IS WRITTEN, n!
6! = 6 • 5 • 4 • 3 • 2 • 1 = 720 3! = 3 • 2 • 1 = 6 1! = 1 and by definition 0! = 1
The band problem has a few important characteristics that our earlier fundamental counting principle problems didn’t have:
1. NO ITEM IS USED MORE THAN ONCE
2. THE ORDER OF THE ARRANGEMENT MAKES A DIFFERENCE.
When these two conditions are involved in the arrangement it is called a PERMUTATION.
|
When does ORDER MATTER? This is an important question!! Order matters when the sequence means something. Jack is runner J, Sally is runner S and Randy is runner R so if they finish the race SJR the order matters because Sally was 1st, Jack came in 2nd, and Randy came in 3rd. If they have finished RSJ, they would receive different prizes and awards. In contrast, if these three runners had been selected to get a $10 gift certificate for finishing in the top three, it wouldn’t have matter if they finished SJR or RSJ – they would all get the same prize and the order wouldn’t matter at all. Order matters when the value or meaning of the location is somehow different from the other locations.
When order matters 123, 132, 213, 231, 312 and 321 are all different possible arrangements for the situation.
If order didn’t matter 123, 132, 213, 231, 312 and 321 are all the same arrangement for the situation.
In the below examples, note that no items can be used more than once and that the order matters. Thus these are examples of PERMUTATIONS.
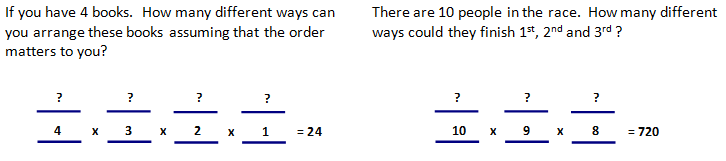
We see a nice pattern forming through this intuitive approach to solving the problem. Each time one less option is available because an item cannot be used more than once. Also if there are more items than things that we are choosing then we only do that many locations.
The above method for calculating permutations is a very intuitive method (but very effective). There is a powerful formula that summarizes exactly what we have been doing above.

CONCEPT 3 – Combination (Order DOESN’T Matters)
Let me introduce another type of problem. A teacher wants to pick 2 students to get the textbooks from the other room. If there are 5 students, how many groups can be formed? What is different about this question from the Permutation questions earlier? ORDER DOESN’T MATTER!! There is no difference to being chosen 1st or 2nd. In this situation, Mike and then Joe is the same as picking Joe and then Mike… the pair of students selected for the group is still Mike and Joe This is known as a COMBINATION.
1. NO ITEM IS USED MORE THAN ONCE
2. THE ORDER OF THE ARRANGEMENT MAKES A NO DIFFERENCE.
(Picking 123 is the same as picking 231 or 321 or 213… etc…. there are always fewer combinations than
permutations because combinations divide out the ‘repeated equivalent’ groups.)
|
We will introduce formulas soon but for now a combination is determined by finding the permutations (all arrangements) and then dividing out the duplication by dividing by r!, where r is the grouping size.

We notice that this is the same process as determining a permutation EXCEPT WE DIVIDE OUT THE DUPLICATION. This helps us to alter the formula for permutations into one that will calculate the combinations.

CONCEPT 4 – Permutations & Combinations with a Calculator
Most graphing calculators have these relationships pre-programed into the calculator. Let me show you were these special probability operations can be found.

CONCEPT 5 – Permutations & Combinations and Probabilities
The main reason we have looked at permutations and combinations is to help us determine how many possible things can happen. These relationships help us with more complex probabilities.
Example #1
There are 10 men and 4 women applying to be members of a 3 person committee. What is the probability that 3 women will be selected?

Example #2
A BIG BUCKS lottery has participants choosing 6 different numbers from numbers 1 to 59. If all six numbers are chosen at random, then the winner receives 10,000,000!!!! Jack pays $100 to get 100 tickets, what are his chances of winning?
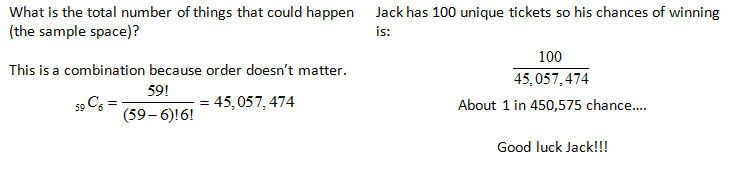
Example #3
8 Nuclear Physicists and 5 Nuclear Chemists have all applied to be on the next NASA team of 5 lead scientists. What is the probability that 3 Physicists and 2 Chemists are chosen?

|