CONCEPT 1 - Prove theorems about parallelograms.
| TEACHER NOTE -- I have provided a number of different ways to prove these concepts, both traditional and transformational. This allows for flexibility on your part to determine the rigor and style of the proof. |
(1) Prove that opposite sides of a parallelogram are congruent.
a) Proof by Symmetry and Patty Paper (Informal – Transformational Approach)

b) Proof by Congruent Triangles (Formal – Classic Approach)

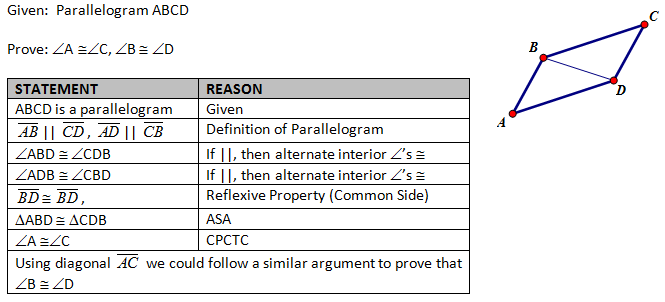
(2) Prove that opposite angles of a parallelogram are congruent.
| TEACHER NOTE -- Notice how the symmetry that we established in G.CO.3 is showing up here to help us establish properties of parallelograms. |
a) Proof by Symmetry and Patty Paper (Informal – Transformational Approach)

b) Proof by Congruent Triangles (Formal – Classic Approach)
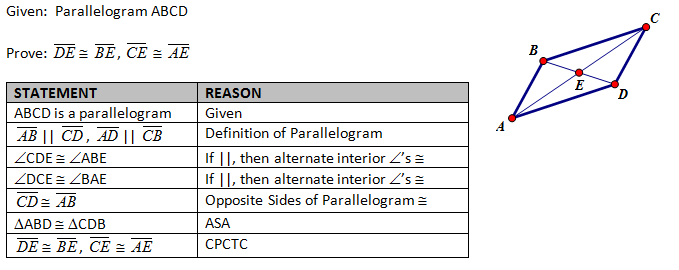
(3) Prove that diagonals bisect each other in a parallelogram.
a) Proof by Symmetry and Patty Paper (Informal – Transformational Approach)

b) Proof by Congruent Triangles (Formal – Classic Approach)
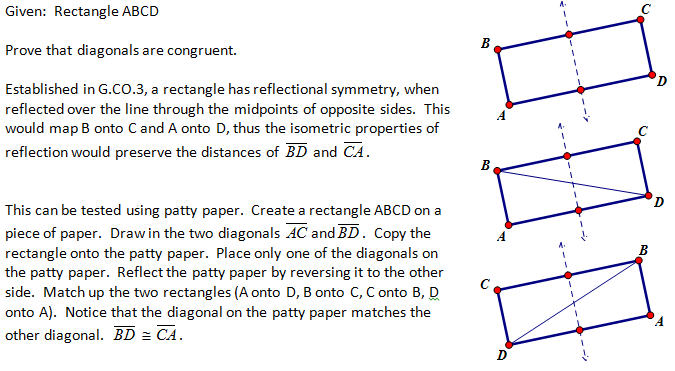
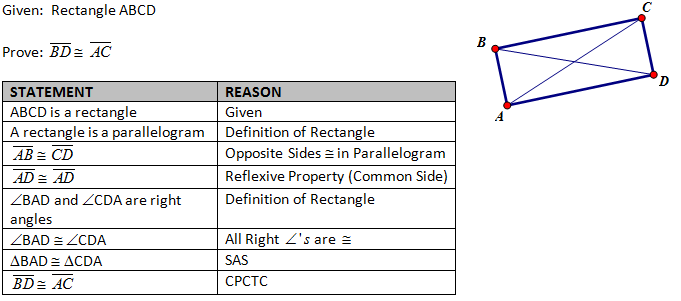
4. Prove that diagonals are congruent in a rectangle.
a) Proof by Symmetry and Patty Paper (Informal – Transformational Approach)
b) Proof by Triangle Congruence (Formal – Classic Approach)
5. Prove that the diagonals of a rhombus are angle bisectors.
a) Proof by Symmetry and Patty Paper (Informal – Transformational Approach)

b) Proof by Triangle Congruence (Formal – Classic Approach)
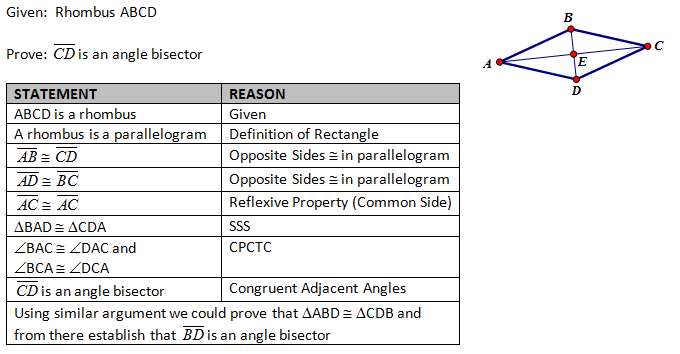
6. Prove that the diagonals of a rhombus are perpendicular.
a) Proof by Symmetry and Patty Paper (Informal – Transformational Approach)

b) Proof by Triangle Congruence (Formal – Classic Approach)

CONCEPT 2 - Conversely, Establish when a quadrilateral is a parallelogram.
| TEACHER NOTE -- The converse arguement on these is essential. Identifying when something is a parallelogram is a major help to proving many other concepts. We will also use these converse arguements when doing coordinate proof to determine the type of quadrilateral that we are looking at. |
(1) If a quadrilateral has two sets of opposite parallel sides.
By definition, it must be a parallelogram.
(2) If a quadrilateral has two sets of opposite congruent sides.

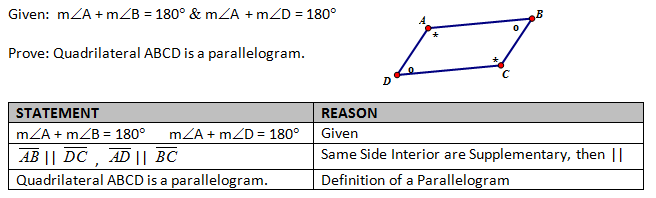
(3) If a quadrilateral has two sets of opposite congruent angles.
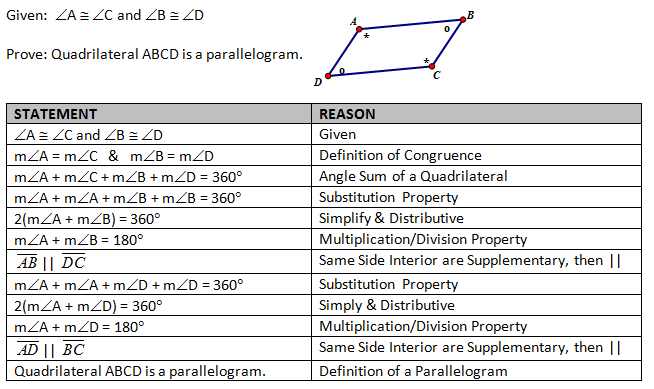
(4) If a quadrilateral has consecutive interior angles that are supplementary.
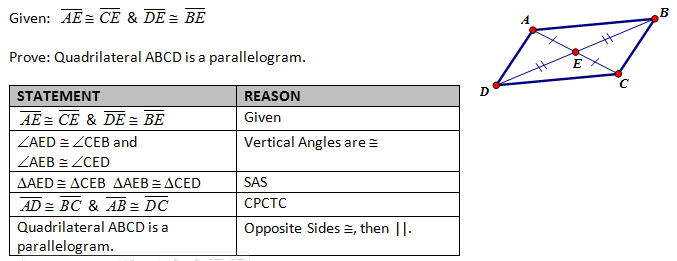
(5) If a quadrilateral has diagonals that bisect each other.
(6) if a quadrilateral has one set of opposite sides that are BOTH parallel and congruent.

TO ESTABLISH IF A QUADRILATERAL IS A PARALLELOGRAM
- Both pairs of opposite sides are parallel.
- Both pairs of opposite sides are congruent.
- Both pairs of opposite angles are congruent.
- Consecutive angles are supplementary.
- Diagonals bisect each other.
- One pair of opposite sides is both congruent and parallel.
|


















