| |
|
|
 |
|
|
| |
|
|
1. Which of the following is NOT a characteristic of all parallelograms?
A) Opposite angles are supplementary B) Opposite angles are congruent
C) Opposite sides are parallel D) Opposite sides are congruent
|
| |
|
|
2. Which of the following is not a special type of parallelogram?
A) Square B) Rhombus
C) Rectangle D) Isosceles Trapezoid
|
| |
|
|
3. Which of the following is NOT a characteristic of all rectangles?
A) Diagonals bisect each other B) Opposite sides are congruent
C) Diagonals are perpendicular D) Four congruent angles
|
| |
|
|
4. Which of the following group of quadrilaterals have diagonals that are perpendicular?
A) Rhombus, Square B) Rhombus, Parallelogram, Square
C) Rectangle, Square D) Rectangle, Rhombus, Square
|
| |
|
|
| 5. A rectangle has diagonals that bisect each other. T or F |
| |
|
|
| 6. If you have 4 congruent angles and 4 congruent sides you must be a square. T or F |
| |
|
|
| 7. Consecutive sides are congruent in a rectangle. T or F |
| |
|
|
 |
|
|
| |
|
|
8 Make a quadrilateral by rotating ΔRST 180° about U.
What type of quadrilateral is formed?
RECTANGLE
What did you see in the shape to conclude the type of quadrilateral? |
 |
|
| x + o = 90°, thus 4 right angles |
|
 |
| |
|
|
| |
|
|
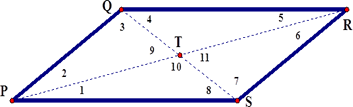
9. What are the missing measures in Parallelogram SRQP?
m∠9 = 66˚ m∠2 = 14˚ m∠1 = 16˚
m∠6 = 14° m∠10 = 114°
m∠11 = 66° m∠3 = 100° |
 |
|
| |
|
|
 |
|
|
| |
|
|
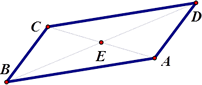
10. Prove that the opposite sides of a parallelogram are congruent using a transformational approach.
Given: Parallelogram ABCD, E is the center of the parallelogram. |
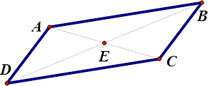 |
Established in G.CO.3, a parallelogram has rotational symmetry, when rotated about its center 180°.
Rotational symmetry would map 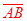 onto onto 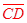 and and 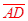 onto onto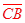 , thus making them congruent. , thus making them congruent.
This can be tested using patty paper. Create a parallelogram ABCD on a piece of paper. Draw in the two diagonals 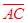 and and 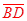 to determine the intersection E. to determine the intersection E.
Copy the parallelogram onto the patty paper. Line up the two parallelograms and then pin the patty paper with your pencil at E and begin to rotate the patty paper. At a 180° rotation, you will see that 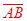 ≅ ≅ and and  ≅ ≅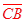 . . |

|
|
| |
|
|
| |
|
|
 |
|
 |
| |
|
Questions developed for Objective G.CO.11 |
I have provided an amazing amount of resources on this site to help you to succeed in teaching common core geometry. That is my goal - that you and I make it through this difficult transition!!
I have held back giving out my:
- notes (in an editable form),
- my worksheets & their answer keys,
- my activities,
- and my assessments & their keys.
The purchase of these items, accompanied by the materials on the site, will provide you with a smooth year of teaching.
GO TO THE SUPPORT PAGE TO LEARN MORE |
|
|
| |
MULTIPLE CHOICE -- 18 questions |
| |
|
| |
TRUE/FALSE -- 16 questions |
| |
|
| |
SHORT ANSWER -- 6 questiions |
| |
|
| |
LONG ANSWER -- 4 questions |
| |
|
| |
CHECK OUT THE BANK |
| |
|
| |
|
| |
|
| |
|
|










