CONCEPT 1 -Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular line, parallel lines, and line segment.
THE ISOMETRIC TRANSFORMATIONS
(1) THE REFLECTION
EXPLANATION
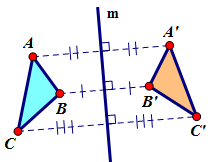 A reflection over a line m (notation Rm) is an isometric transformation in which each point of the original figure (pre-image) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line. Because a reflection is an isometry, the image does not change size or shape. The line of reflection is the perpendicular bisector of the segment joining every point and its image. A reflection over a line m (notation Rm) is an isometric transformation in which each point of the original figure (pre-image) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line. Because a reflection is an isometry, the image does not change size or shape. The line of reflection is the perpendicular bisector of the segment joining every point and its image.
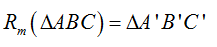
DEFINITION
A reflection in a line m is a isometric transformation that maps every point P in the plane to a point P’, so that the following properties are true; |
1. If point P is NOT on line m, then line m is the perpendicular bisector of  . . |
2. If point P is ON line m, then P = P’ |
 |
| TEACHER NOTE -- Each of these transformations have ISOMETRIC properties and TRANSFORMATION properties. The isometric properites help us build concepts to congruence, and the transformation properties help us understand the specific properties of that motion in the plane. |
PROPERTIES
ISOMETRIC PROPERTIES - Because a reflection is an isometric transformation the following properties are preserved between the pre-image and its image:
- Distance (lengths of segments are the same)
- Angle measure (angles stay the same)
- Parallelism (things that were parallel are still parallel)
- Collinearity (points on a line, remain on the line)
After a reflection, the pre-image and image are identical.
TRANSFORMATION PROPERTIES – Because a reflection is a transformation that maps all points the perpendicular distance on the opposite side of the line of reflection the following properties are present.
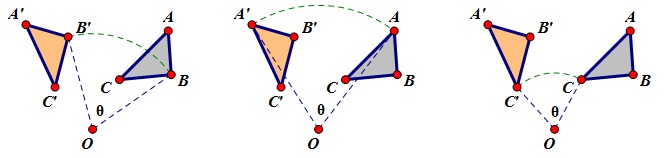
 DISTANCES ARE DIFFERENT -- Points in the plane move different distances, depending on their distance from the line of reflection. Points farther away from the line of reflection move a greater distance than those closer to the line of reflection. Notice how AA’ is greater than BB’. Notice that because line m is the perpendicular to DISTANCES ARE DIFFERENT -- Points in the plane move different distances, depending on their distance from the line of reflection. Points farther away from the line of reflection move a greater distance than those closer to the line of reflection. Notice how AA’ is greater than BB’. Notice that because line m is the perpendicular to 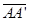 , , 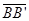 and and 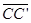 they are all parallel to each other. they are all parallel to each other.
- ORIENTATION IS REVERSED – The pre-image has a reversed orientation than its image. Orientation is the order of the points about the shape. In DABC the points in a clockwise direction come in the order of A – B – C but in the image the points in a clockwise direction come in the order of A’ – C’ – B’. This occurs because a reflection creates the mirror image.
- SPECIAL POINTS – Points on the line of reflection do not move at all under the reflection. The pre-image (D) = image (D’) when the point is on the line of reflection.
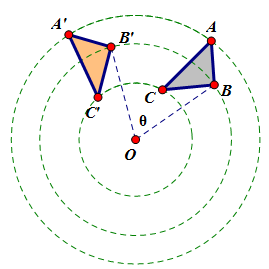 (2) THE ROTATION (2) THE ROTATION
EXPLANATION
A rotation is an isometric transformation that turns a figure about a fixed point called the center of rotation. Rays drawn from the center of rotation to a point and its image form an angle called the angle of rotation
(notation Rcenter, degree).
An object and its rotation are the same shape and size, but the figures may be turned in different directions.

DEFINITION
A rotation about a Point O through Θ degrees is an isometric transformation that maps every point P in the plane to a point P’, so that the following properties are true; |
1. If point P is NOT point O, then OP = OP’
and m∠QPQ’ = Θ°. |
2. If point P IS point O, then P = P’. The center of rotation is the ONLY point in the plane that is unaffected by a rotation. |
 |
| TEACHER NOTE -- Direction of rotation is a difficult for students to get correct. They always think positive is clockwise... beware!! |
ROTATION DIRECTION
One full rotation is 360°, this would return all points in the plane to their original location. Because a rotation can go in two directions along the same arc we need to define positive and negative rotation values. COUNTERCLOCKWISE IS A POSITIVE DIRECTION, and clockwise is a negative direction.

Students often want to know why this ‘backwards’ relationship happens….. my belief is that the rotation direction comes from the coordinate plane, In the coordinate plane, the initial arm of the angle is the positive x axis, and the terminal arm opens in a counterclockwise direction from there.
EQUIVALENT ROTATIONS
Because angles are formed along an arc of a circle there are two ways to get to the same location, a positive direction and a negative direction. A 60° rotation is the same as a -300° rotation. Co-terminal angles can be calculated using the formula, a coterminal angle = initial angle + 360n, where n is an integer.
60° = 60° + (1)360° = 420° 60° = 60° + (2)360° = 780°
60° = 60° + (-1)360° = -300° 60° = 60° + (-2)360° = -660°
Conterminal angle = initial angle + 360n
PROPERTIES
ISOMETRIC PROPERTIES - Because a rotation is an isometric transformation the following properties are preserved between the pre-image and its image:
- Distance (lengths of segments are the same)
- Angle measure (angles stay the same)
- Parallelism (things that were parallel are still parallel)
- Collinearity (points on a line, remain on the line)
After a rotation, the pre-image and image are identical.
 TRANSFORMATION PROPERTIES – Because a rotation is a transformation that maps all points along an arc the following properties are present. TRANSFORMATION PROPERTIES – Because a rotation is a transformation that maps all points along an arc the following properties are present.
- DISTANCES ARE DIFFERENT -- Points in the plane move different distances, depending on their distance from the center of rotation. A point farther away from the center of rotation maps a greater distance than those points closer to the center of rotation. Notice that different from a reflection,
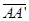 , , 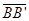 and and 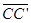 are NOT parallel to each other. are NOT parallel to each other.
- ORIENTATION IS THE SAME – The pre-image has the same orientation as its image. Orientation is the order of the points about the shape. In DABC the points in a clockwise direction come in the order of A – B – C and in the image the points in a clockwise direction come in the order of A’ – B’ – C’. They are the same!! (Sometimes students want to say that a rotation changes the orientation of the shape because the shape has been turned to create a different look of the shape…. this is NOT an orientation change!)
- SPECIAL POINTS – The center of rotation is the only point in the plane that is unchanged, O = O’.
| TEACHER NOTE -- The 180° rotation will help us prove and identify many new things in the future. Make sure this definition is well understood. |
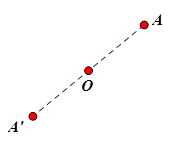
SPECIAL ROTATION – ROTATION OF 180°
A rotation of 180° maps A to A’ such that:
a) m∠AOA’ = 180° (from definition of rotation)
b) OA = OA’ (from definition of rotation)
c) Ray 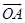 and Ray and Ray  are opposite rays. (They form a line.) are opposite rays. (They form a line.)
 is the same line as is the same line as 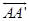 |
 |
(3) THE TRANSLATION
EXPLANATION
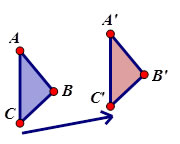 A translation slides an object a fixed distance in a given direction. When working in the plane this is usually represented by an arrow, the arrow provides both distance and direction of the translation. When working on the coordinate plane, a vector is used to describe the fixed distance and the given direction often denoted by <x,y>. The x value describes the effect on the x coordinates (right or left) and the y value describes the effect on the y coordinates (up or down). A translation slides an object a fixed distance in a given direction. When working in the plane this is usually represented by an arrow, the arrow provides both distance and direction of the translation. When working on the coordinate plane, a vector is used to describe the fixed distance and the given direction often denoted by <x,y>. The x value describes the effect on the x coordinates (right or left) and the y value describes the effect on the y coordinates (up or down).
The pre-image and image have the same shape and size.

DEFINITION
A translation is an isometric transformation that maps every two points A and B in the plane to points A’ and B’, so that the following properties are true;
|
1. AA’ = BB’ (a fixed distance).
2. 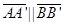 (a fixed direction). (a fixed direction). |
 |
PROPERTIES
ISOMETRIC PROPERTIES - Because a translation is an isometric transformation the following properties are preserved between the pre-image and its image:
- Distance (lengths of segments are the same)
- Angle measure (angles stay the same)
- Parallelism (things that were parallel are still parallel)
- Collinearity (points on a line, remain on the line)
After a translation, the pre-image and image are identical.
 TRANSFORMATION PROPERTIES – Because a translation is a transformation that maps all a fixed distance and in a fixed direction the following properties are present. TRANSFORMATION PROPERTIES – Because a translation is a transformation that maps all a fixed distance and in a fixed direction the following properties are present.
- DISTANCES ARE THE SAME -- Points in the plane all map the exact same distance. Notice how AA’ is EQUAL TO BB’.
- ORIENTATION IS THE SAME – The pre-image has the same orientation as its image. In DABC the points in a clockwise direction come in the order of A – B – C and in the image the points in a clockwise direction come in the order of A’ – B’ – C’.
- SPECIAL POINTS – There are NO special points, ALL POINTS IN THE PLANE MOVE!!!
| TEACHER NOTE -- The translation along an angles ray will help us prove and identify many new things in the future. Make sure this definition is well understood. It will connect us into parallel lines and a transversal. |
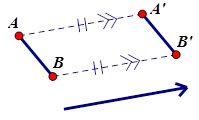
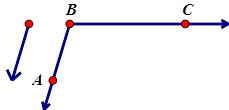
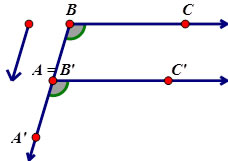
SPECIAL TRANSLATION PROPERTY – TRANSLATING AN ANGLE ALONG ONE OF ITS RAYS
A translation of ∠ABC by vector 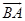 maps all points such that maps all points such that
1. ∠ABC ≅ ∠A’B’C’ (Isometry)
2. B, A, B’ and A’ are collinear (translation on angle ray)
Because the two angles are equal and formed on the same ray, then:
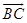 || ||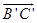
This is a key property to translations –
All segments that are translated are parallel to each other. |
|
|


 A reflection over a line m (notation Rm) is an isometric transformation in which each point of the original figure (pre-image) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line. Because a reflection is an isometry, the image does not change size or shape. The line of reflection is the perpendicular bisector of the segment joining every point and its image.
A reflection over a line m (notation Rm) is an isometric transformation in which each point of the original figure (pre-image) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line. Because a reflection is an isometry, the image does not change size or shape. The line of reflection is the perpendicular bisector of the segment joining every point and its image.
 DISTANCES ARE DIFFERENT -- Points in the plane move different distances, depending on their distance from the line of reflection. Points farther away from the line of reflection move a greater distance than those closer to the line of reflection. Notice how AA’ is greater than BB’. Notice that because line m is the perpendicular to
DISTANCES ARE DIFFERENT -- Points in the plane move different distances, depending on their distance from the line of reflection. Points farther away from the line of reflection move a greater distance than those closer to the line of reflection. Notice how AA’ is greater than BB’. Notice that because line m is the perpendicular to  (2) THE ROTATION
(2) THE ROTATION


 TRANSFORMATION PROPERTIES – Because a rotation is a transformation that maps all points along an arc the following properties are present.
TRANSFORMATION PROPERTIES – Because a rotation is a transformation that maps all points along an arc the following properties are present.
 A translation slides an object a fixed distance in a given direction. When working in the plane this is usually represented by an arrow, the arrow provides both distance and direction of the translation. When working on the coordinate plane, a vector is used to describe the fixed distance and the given direction often denoted by <x,y>. The x value describes the effect on the x coordinates (right or left) and the y value describes the effect on the y coordinates (up or down).
A translation slides an object a fixed distance in a given direction. When working in the plane this is usually represented by an arrow, the arrow provides both distance and direction of the translation. When working on the coordinate plane, a vector is used to describe the fixed distance and the given direction often denoted by <x,y>. The x value describes the effect on the x coordinates (right or left) and the y value describes the effect on the y coordinates (up or down).
 TRANSFORMATION PROPERTIES – Because a translation is a transformation that maps all a fixed distance and in a fixed direction the following properties are present.
TRANSFORMATION PROPERTIES – Because a translation is a transformation that maps all a fixed distance and in a fixed direction the following properties are present.
