CONCEPT 1 -- Prove theorems about lines and angles.
A) Vertical angles are congruent.
When we defined a rotation we looked at the properties of the special rotation of 180°.

| TEACHER NOTE -- I love how we approach this from a transformational standpoint... it is fresh and new. It also shows how easy this is when we prepare this concept back in G.CO.4. I would suggest doing this proof before G.CO.8 so that you can use vertical angles are congruent when proving congruent triangles. This is not a difficult proof and can happen any time after G.CO.4. |
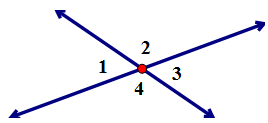
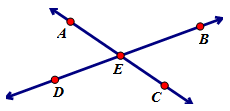
This will help us prove the relationship between two vertical angles. First of all, vertical angles are the two non-adjacent angles formed by intersecting lines. So in the diagram ∠1 and ∠3 are vertical angles and ∠2 and ∠4 are vertical angles as well. |
 |
| |
|
To Prove that Vertical Angles are Congruent we use the properties of an 180° rotation.
Prove: ∠DEA ≅ ∠BEC
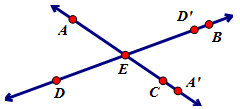
A rotation of 180° about point E, maps D onto . D’ lies on . D’ lies on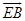 . .
A rotation of 180° about point E, maps A onto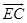 . A’ lies on . A’ lies on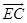 . .
∠D’EA’ ≅ ∠BEC because the angles use the same rays and vertex.
Thus using the transitive property, ∠DEA ≅ ∠BEC.
Using a similar argument we could also prove, ∠DEC ≅ ∠BEA.
|
|

B) When a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent.
To prove this relationship we are also going to go back to the properties of a translation of an angle along one of its rays.

| TEACHER NOTE -- Another nice example of how the transformations introduce these concepts in a new way. Developing strong definitions early on in G.CO.4 helps here again. The proofs of alternate interior, alternate exterior, consecutive interior and conseuctive exterior have all been done algebraically because they are very simple and visual but they could also be done through transformations. For example proving two alternate exterior are congruent, you could perform a translation down the transversal and then a rotation of 180°. |
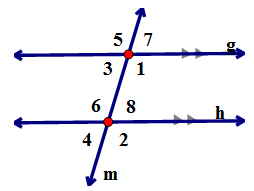
The translation of angles ∠1, ∠3, ∠5 & ∠7 along the transversal line m give us congruent corresponding angles, ∠2, ∠4, ∠6 & ∠8.
This angle relationship is called CORRESPONDING ANGLES and because of the properties of the isometric translation, CORRESPONDING ANGLES MUST BE CONGRUENT.
∠1 ≅ ∠2, ∠3 ≅ ∠4, ∠5 ≅ ∠6 & ∠7 ≅ ∠8 |
 |
| |
|
∠5 & ∠2 and ∠7 & ∠4 are called ALTERNATE EXTERIOR ANGLES. Alternate because they are on alternating sides of the transversal and exterior because they are on the outside of the parallel lines.
PROVE: ALTERNATE EXTERIOR ANGLES ARE CONGRUENT
PROVE: ∠4 ≅∠7 & ∠2 ≅∠5
∠4 ≅ ∠3 because corresponding angles are congruent and
∠3 ≅ ∠7 because vertical angles are congruent.
Thus using the transitive property, ∠4 ≅ ∠7. We could use a similar argument to prove ∠2 ≅ ∠5. |
 |
| |
|
∠3 & ∠8 and ∠6 & ∠1 are called ALTERNATE INTERIOR ANGLES. Alternate because they are on alternating sides of the transversal and interior because they are on the interior of the parallel lines.
PROVE: ALTERNATE INTERIOR ANGLES ARE CONGRUENT
PROVE: ∠3 ≅∠8 & ∠6 ≅∠1
∠3 ≅ ∠4 because corresponding angles are congruent and
∠4 ≅ ∠8 because vertical angles are congruent.
Thus using the transitive property, ∠3 ≅ ∠8. We could use a similar argument to prove ∠6 ≅ ∠1. |
 |
| |
|
∠3 & ∠6 and ∠1 & ∠8 are called CONSECUTIVE INTERIOR ANGLES (OR SAME SIDE INTERIOR ANGLES). I prefer same side…. Same Side because they are on the same side of the transversal and interior because they are on the interior of the parallel lines.
PROVE: SAME SIDE INTERIOR ANGLES ARE SUPPLEMENTARY
PROVE: m∠1 + m∠8 = 180° & m∠3 + m∠6 = 180°
m∠1 + m∠7 = 180° because they are a linear pair and
m∠7 = m∠8 because corresponding are congruent.
If we substitute, we get m∠1 + m∠8 = 180°.
We could use a similar argument to prove m∠3 + m∠6 = 180°. |
 |
| |
|
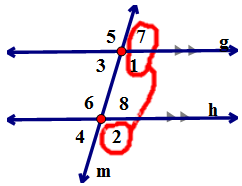
∠3 & ∠6 and ∠1 & ∠8 are called CONSECUTIVE EXTERIOR ANGLES (OR SAME SIDE EXTERIOR ANGLES). I prefer same side…. Same Side because they are on the same side of the transversal and exterior because they are on the exterior of the parallel lines.
PROVE: SAME SIDE EXTERIOR ANGLES ARE SUPPLEMENTARY
PROVE: m∠2 + m∠7 = 180° & m∠4 + m∠5 = 180°
m∠1 + m∠7 = 180° because they are a linear pair and
m∠1 = m∠2 because corresponding are congruent.
If we substitute, we get m∠2 + m∠7 = 180°.
We could use a similar argument to prove m∠4 + m∠5 = 180°. |
 |
| |
|
 |
| |
|
C) Points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.
| TEACHER NOTE -- Again I choose here not to approach this proof using the typical use of triangle congruence. I use the definition of a reflection to establish that the perpendicular bisector is the line of reflection and due to the isometric properties all points C on the perpendicular bisector will equidistant to the endpoints of the segment. |
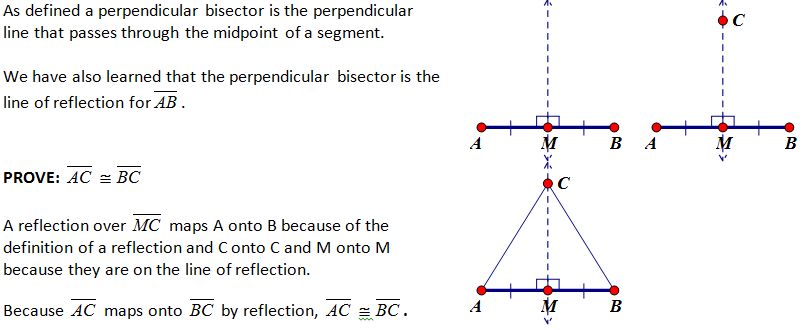
Another way to prove this might be to prove the two triangles are congruent. The common side, the bisected segment and the right angle give us a SAS relationship.
| TEACHER NOTE -- Pairs of angles are not specifically stated in the objective but this is a good time to clarify a few relationships that will be used in following objectives. |
CONCEPT 2 – PAIRS OF ANGLES
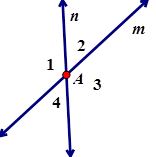 It is very common for two lines to intersect in the plane. When two lines intersect a point is formed and also a number of angles. In the diagram to the right, the intersection of line m and line n is point A. The angles formed have many different names and relationships. It is very common for two lines to intersect in the plane. When two lines intersect a point is formed and also a number of angles. In the diagram to the right, the intersection of line m and line n is point A. The angles formed have many different names and relationships.
The diagram to the right has some Adjacent Angles.
ADJACENT ANGLES are angles that share a vertex and a ray and no interior points. So in the diagram to the right Ð1 & Ð2 are adjacent angles. There are other examples of adjacent angles in the diagram such as ∠4 & ∠1.
The diagram to the right has some Linear Pairs.
A LINEAR PAIR are two angles that are adjacent and sum to 180°. In this particular diagram Ð1 & Ð2 are more specifically called a linear pair. ∠2 & ∠3, ∠3 & ∠4, and ∠4 & ∠1 are also a linear pairs.
The diagram to the right has some Vertical Angles.
VERTICAL ANGLES are a pair of non-adjacent angles formed by the intersection of two lines. The angles labeled ∠1 & ∠3 and ∠2 & ∠4 are vertical angles.
SUPPLEMENTARY ANGLES – Two angles are supplementary if the sum of their measures is 180°. All linear pairs are supplementary but not all supplementary angles are linear pairs. Linear pairs are the specific cases when the two supplemenary angles are adjcent and thus form a line. Supplement angles in general do not have to be adjacent.
COMPLEMENTARY ANGLES – Two angles are complementary if the sum of their measures is 90°. An example of complements are the two acute angles in a right triangle. The right triangle is 90° and the remaining two angles sum to 90.
|















 It is very common for two lines to intersect in the plane. When two lines intersect a point is formed and also a number of angles. In the diagram to the right, the intersection of line m and line n is point A. The angles formed have many different names and relationships.
It is very common for two lines to intersect in the plane. When two lines intersect a point is formed and also a number of angles. In the diagram to the right, the intersection of line m and line n is point A. The angles formed have many different names and relationships.