| |
|
|
 |
|
|
| |
|
|
1. Determine the pair of vertical angles.
A) ∠DCF & ∠ACB B) ∠BCF & ∠ACE
C) ∠FCD & ∠ACE D) ∠BCA & ∠ECD |
 |
|
| |
|
|
2. If 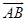 bisects ∠CAF, and m∠EAF = 66°, then the m∠BAF = bisects ∠CAF, and m∠EAF = 66°, then the m∠BAF =
A) 33° B) 57° C) 66° D) 114° |
 |
|
| |
|
|
3. If m∠1 = 48° and m∠2 = 4x + 4 , then:
A) x = 11 B) x = 13 C) x = 32 D) x = 34 |
 |
|
| |
|
|
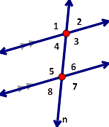
4. Determine the correct name for ∠4 and ∠5.
A) Same Side Interior B) Alternate Interior Angles
C) Alternate Exterior Angles D) Linear Pair |
 |
|
| |
|
|
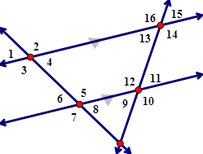
5. Determine the correct name for ∠9 and ∠15.
A) Same Side Interior B) Alternate Interior Angles
C) Alternate Exterior Angles D) Corresponding Angles |
 |
|
| |
|
|
| 6. If ∠A and ∠B are vertical angles, then if m∠A = 3x, then m∠B = 5x -2x. T or F |
| |
|
|
| 7. If ∠A and ∠B are a vertical angles, then ∠A and ∠B are also adjacent angles. T or F |
| |
|
|
| 8. When two parallel lines intersect a transversal, same side interior angles are ≅. T or F |
| |
|
|
9. if 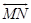 is the ⊥ bisector of is the ⊥ bisector of 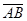 , and G is on , and G is on 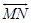 , then , then  . T or F . T or F |
| |
|
|
 |
|
|
| |
|
|
10. Match the following.
a) __(5)__ Straight Angle 1. Two angles that sum to 180.
b) __(7)__ Acute Angle 2. Two nonadjacent angles formed by intersecting lines.
c) __(8)__ Obtuse Angle 3. Has an angle measure of 90.
d) __(3)__ Right Angle 4. Two angles that sum to 90.
e) __(6)__ Adjacent Angle 5. Has an angle measure of 180
f) __(2)__ Vertical Angles 6. Angles that share a vertex & a ray & no interior.
g) __(4)__ Complementary Angles 7. Has an angle measure of less than 90.
h) __(1)__ Supplementary Angle 8. Has an angle measure > 90 & < 180. |
| |
|
|
 |
|
|
| |
|
|
| 11. A teacher asks a student to ‘prove’ that two vertical angles are congruent. The student draws two intersecting lines on a piece of paper and then folds one vertical angle onto the other. The teacher congratulates the young pupil for a creative way to demonstrate this and then the teacher asks the student to unfold his paper. What is the fold in relation to the two vertical angles that the student demonstrated to be congruent? |
| |
|
|
| The creased fold would be the angle bisector of the adjacent supplementary angle to the two vertical angles. It would also be a line of reflection for the two vertical angles, where the vertex of the two vertical angles lies on the line of reflection. |
 |
|
| |
|
|
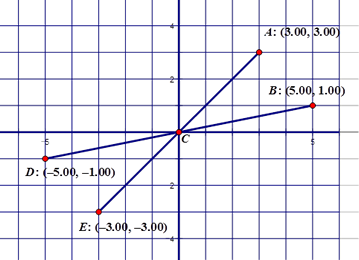
12. In class we discussed how the definition for vertical angles did not include that all vertical angles were congruent to each other. We had to prove that ourselves in class. Below provide an explanation (a proof) why ∠ACB ≅ ∠ECD. Be as specific (as clear) as possible.
This is a rotation of 180°. The coordinate rule for a rotation of 180° is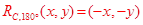 . Thus the image of A is E and the image of B is D and of course the image of C = C. The isometric transformation preserves the angle size…. . Thus the image of A is E and the image of B is D and of course the image of C = C. The isometric transformation preserves the angle size….
Thus ∠ACB ≅ ∠ECD. |
 |
|
| |
 |
|
 |
| |
|
Questions developed for Objective G.CO.9 |
I have provided an amazing amount of resources on this site to help you to succeed in teaching common core geometry. That is my goal - that you and I make it through this difficult transition!!
I have held back giving out my:
- notes (in an editable form),
- my worksheets & their answer keys,
- my activities,
- and my assessments & their keys.
The purchase of these items, accompanied by the materials on the site, will provide you with a smooth year of teaching.
GO TO THE SUPPORT PAGE TO LEARN MORE |
|
|
| |
MULTIPLE CHOICE -- 21 questions |
| |
|
| |
TRUE/FALSE -- 34 questions |
| |
|
| |
SHORT ANSWER -- 15 questiions |
| |
|
| |
LONG ANSWER -- 9 questions |
| |
|
| |
CHECK OUT THE BANK |
| |
|
| |
|
| |
|
| |
|
|












